வெளிச்சில்லுரு
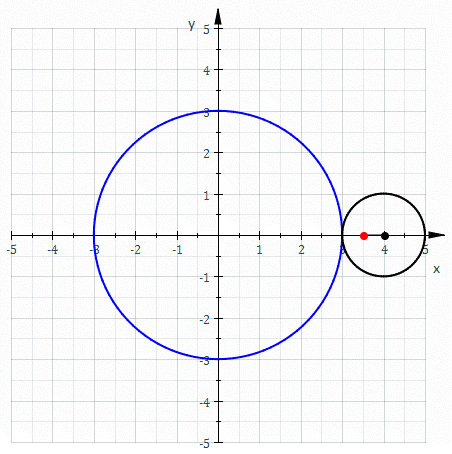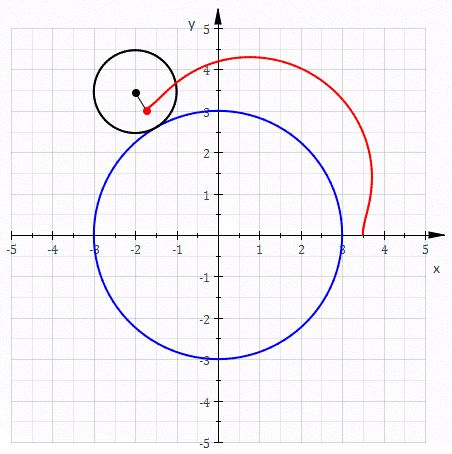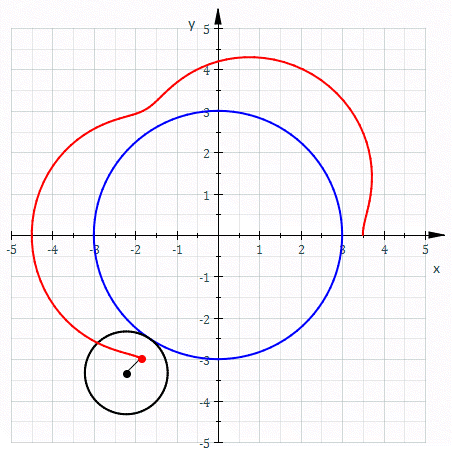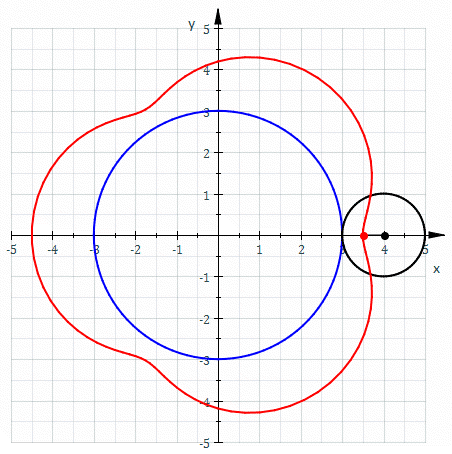
வெளிச்சில்லுரு (epitrochoid) என்பது ஒரு வட்டத்துடன் தொடர்புபடுத்தப்பட்ட புள்ளியொன்றின் தடத்தினைக் காட்டும் சிறுசில்லி (roulette) வகையைச் சேர்ந்த ஒரு வளைவரை. தொடர்புபடுத்தப்பட்ட வட்டத்தின் மையத்துக்கும் அப்புள்ளிக்கும் இடையே உள்ள தூரம் d அலகுகள். இந்த வட்டத்தின் ஆரம் r அலகுகள். இவ்வட்டம் R அலகு ஆரமுள்ள மற்றொரு நிலையான வட்டத்தின் வெளிபுறத்தைத் தொட்டபடியே நழுவாமல் உருளும் போது, நாம் எடுத்துக்கொண்ட புள்ளி நகர்கின்ற தடம் ஒரு வளைவரையாக இருக்கும். சிறுசில்லி வகையைச் சேர்ந்த இவ்வளைவரை, வெளிச்சில்லுரு என அழைக்கப்படுகிறது.
d இன் அளவு r இன் மதிப்பை விடச் சிறியதாகவோ, பெரியதாகவோ அல்லது சமமாகவோஇருக்கலாம். அதாவது புள்ளி வட்டத்துக்குள்ளே, வட்டத்திற்கு வெளியே அல்லது வட்டத்தின் மீது இருக்கலாம். வட்டத்தின் மீது புள்ளி அமையும் போது வெளிச்சில்லுரு, வெளிவட்டப்புள்ளியுருவாக அமையும்.
எடுத்துக்காட்டுகள்[தொகு]
- சுழல் வரைவி -விளையாட்டுக் கருவியால் வரையப்படுவது, வெளிச்சில்லுரு மற்றும் உட்சில்லுரு வளைவரைகள்.
- ஒரு காலத்தில் பரவலாக அறியப்பட்டிருந்த புவிமைய டாலமியின் முறைமையில் கோள்களின் சுற்றுப்பாதைகள் வெளிச்சில்லுரு வடிவில் அமைந்திருப்பதாகக் கருதப்பட்டது.
வெளிச்சில்லுருவின் துணையலகுச் சமன்பாடுகள்[தொகு]
இங்கு ஒரு துணையலகு (போலார் கோணம் அல்ல).
சிறப்பு வகைகள்[தொகு]
- d = r எனில் வெளிச்சில்லுரு ஒரு வெளிவட்டப்புள்ளியுருவாக இருக்கும்.
- R = r எனில் வெளிச்சில்லுரு ஒரு லிமெசன் (limacon) ஆக இருக்கும்.
மேற்கோள்கள்[தொகு]
- J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. பக். 160–164. பன்னாட்டுத் தரப்புத்தக எண்:0-486-60288-5. https://archive.org/details/catalogofspecial00lawr.
வெளி இணைப்புகள்[தொகு]
- Epitrochoid generator
- Epitrochoid at Mathworld
- Visual Dictionary of Special Plane Curves on Xah Lee 李杀网
- Interactive simulation of the geocentric graphical representation of planet paths
- O'Connor, John J.; Robertson, Edmund F., "Epitrochoid", MacTutor History of Mathematics archive, புனித ஆண்ட்ரூசு பல்கலைக்கழகம்.



