பிறை (கணிதம்)
வடிவவியலில் பிறை (lune) என்பது கிட்டத்தட்ட, வளரும் நிலவின் வடிவிலமைந்த இரு உருவங்களில் ஏதாவது ஒன்றினைக் குறிக்கும். நிலவைக் குறிக்கும் luna (லூனா) என்ற இலத்தீன் மொழிச் சொல்லில் இருந்து ஆங்கிலத்தில் இதற்கு லூன் எனப் பெயரிடப்பட்டுள்ளது.
தள வடிவவியல்[தொகு]
தள வடிவவியலில் இரு விற்களால் அடைவுபெற்ற குழிவுப் பரப்பு, பிறையாகும். இதேபோல் இரு விற்களால் அடைவுபெறும் குவிவுப் பரப்பு, வில்லை எனப்படும்.
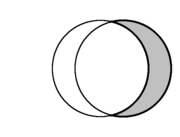
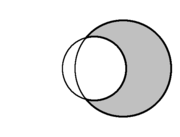
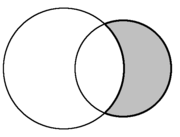
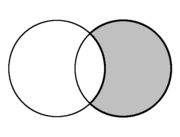
பிறை என்பது இரு வட்டத்தகடுகளில் ஏதாவது ஒரு தகட்டின் (மற்றொரு தகட்டைப் பொறுத்த) நிரப்புகணமாகும், இதில் இருதகடுகளும் ஒன்றுக்கு மற்றது உட்கணமாக இருத்தல் கூடாது.
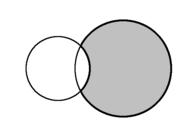
வட்டத் தகடுகள் A மற்றும் B எனில் அவற்றின் பிறை:

|
|
|
|
|
|
| தள வடிவவியலில் இரு வட்டங்களின் வெட்டுப் பகுதி பிறையாகும்.(சாம்பல் நிறம்). | ||
கோள வடிவவியல்[தொகு]

கோள வடிவவியலில் பிறை என்பது, கோளத்தின் இரண்டு அரைப் பெருவட்டங்களால் அடைபெறும் கோளத்தின் மேற்பரப்பாகும்.[1] பெருவட்டம் என்பது ஒரு கோளத்தின் மேல் வரையக்கூடிய மிகப்பெரிய வட்டமாகும். ஒவ்வொரு பெருவட்டமும் கோளத்தின் மேற்பரப்பை இரு சமபாகங்களாகப் பிரிக்கும். இரண்டு பெருவட்டங்கள் எப்பொழுதும் எதிரெதிராக அமையும் இரண்டு முனைப் புள்ளிகளில் வெட்டிக்கொள்ளும். பெருவட்டங்களுக்கு எடுத்துக்காட்டு, பூமியின் மேற்பரப்பின்மீது வடக்கு-தெற்காக, கற்பனையாக வரையப்பட்டுள்ள நெடுவரை(தீர்க்க ரேகை)களாகும். இரு நெடுவரைகள் பூமியின் மேற்பரப்பில் வட-தென் துருவ முனைப் புள்ளிகளில் சந்திக்கும். எனவே இரு நெடுவரைகளுக்கு இடையேயுள்ள பரப்பு ஒரு பிறையாகும். ஒரு கோளப் பிறையின் பரப்பு 2θ R2 ஆகும். இங்கு, R -கோளத்தின் ஆரம். மற்றும் θ -இரு அரைப் பெருவட்டங்களுக்கு இடையேயுள்ள கோணமாகும். இந்தக் கோணத்தின் அளவு 2π எனில், அதாவது இரண்டாவது அரைப் பெருவட்டமானது முழுச்சுற்றாக நகர்ந்தால், பிறை கோளமாகி மாறிவிடும். இந்நிலையில் பிறையின் பரப்பு 4πR2-கோளத்தின் பரப்பாகும்.


பூமியிலிருந்து பார்க்கக்கூடிய நிலவின் வெளிச்சமான பகுதி ஒரு கோளப்பிறையாகும். வெட்டிக்கொள்ளும் இரு பெருவட்டங்களில் ஒன்று சூரியனால் வெளிச்சம் பெறும் நிலவின் பகுதியையும் இருண்ட பகுதியையும் பிரிக்கும் பெருவட்டமாகும். இரண்டாவது பூமியிலிருந்து பார்க்கக்கூடிய மற்றும் பார்க்க முடியாத நிலவின் பகுதிகளைப் பிரிக்கும் பெருவட்டமாகும். இந்த முப்பரிமாண கோளப்பிறையானது பூமியிலிருந்து பார்க்கப்படும் பொழுது இருபரிமாண வீழ்ச்சியாக தோற்றமளிக்கிறது. படத்தில் உள்ளதைப்போல ஒரு அரைவட்டமும் அந்த வட்டத்தின் விட்டத்தைப் பேரச்சாகக் கொண்ட அரை நீள்வட்டமும் வெட்டிக்கொள்ளும் பகுதியாக பிறை நிலா நம் கண்களுக்குத் தெரிகிறது.
ஹிப்போக்கிரட்டீசின் பிறை[தொகு]

கிமு 5-ம் நூற்றாண்டில் கிரேக்க கணிதவியலாளர் ஹிப்போக்கிரட்டீஸ் ஆஃப் காஸ், சில பிறைகளை நேர்விளிம்பு மற்றும் கவராயம் கொண்டு சதுரப்படுத்த முடியும் எனக் காட்டியுள்ளார். படத்திலில் உள்ள நிழலிடப்பட்ட பகுதியின் பரப்பு -ன் பரப்புக்குச் சமம். இது வட்டத்தைச் சதுரமாக்கும் கேள்விக்கு முழுமையான தீர்வு இல்லை.(முழுமையான தீர்வை, நேர்விளிம்பு மற்றும் கவராயம் கொண்டு காண்பது சாத்தியமல்ல என்பது நிறுவப்பட்டுள்ளது.)
மேற்கோள்கள்[தொகு]
- ↑ Weisstein, Eric W., "SphericalLune", MathWorld.
வெளி இணைப்புகள்[தொகு]
- The Five Squarable Lunes at MathPages



