யூக்ளீடிய வடிவவியலில் பிரம்மகுப்தரின் வாய்ப்பாடு என்பது (Brahmagupta's formula ) வட்ட நாற்கரத்தின் பரப்பளவு காணும் வாய்ப்பாடு ஆகும். ஒரு வட்ட நாற்கரத்தின் பக்கங்களின் நீளங்கள் தரப்பட்டிருக்கும் போது இவ்வாய்ப்பாட்டைப் பயன்படுத்தி அந்த வட்ட நாற்கரத்தின் பரப்பைக் காணலாம்.
அடிப்படைப் படிவம் [ தொகு ] பிரம்மகுப்தரின் வாய்ப்பாட்டின் எளிமையானதும் எளிதில் மனதில் பதியக்கூடியதுமான படிவம், a , b , c , d -ஐ பக்க நீளங்களாகக் கொண்ட வட்ட நாற்கரத்தின் பரப்பைத் தருகிறது:
K
=
(
s
−
a
)
(
s
−
b
)
(
s
−
c
)
(
s
−
d
)
{\displaystyle K={\sqrt {(s-a)(s-b)(s-c)(s-d)}}}
இங்கு s , நாற்கரத்தின் அரைச்சுற்றளவு .
s
=
a
+
b
+
c
+
d
2
⋅
{\displaystyle s={\frac {a+b+c+d}{2}}\cdot }
s
−
a
=
−
a
+
b
+
c
+
d
2
{\displaystyle s-a={\frac {-a+b+c+d}{2}}}
s
−
b
=
a
−
b
+
c
+
d
2
{\displaystyle s-b={\frac {a-b+c+d}{2}}}
s
−
c
=
a
+
b
−
c
+
d
2
{\displaystyle s-c={\frac {a+b-c+d}{2}}}
s
−
d
=
a
+
b
+
c
−
d
2
{\displaystyle s-d={\frac {a+b+c-d}{2}}}
இவ்வாய்ப்பாடு முக்கோணத்தின் பரப்பு காணும் ஹீரோனின் வாய்ப்பாட்டின் பொதுமைப்படுத்தப்பட்டப் படிவமாக அமைகிறது. பிரம்மகுப்தரின் வாய்ப்பாட்டில் d -ன் மதிப்பு பூச்சியத்தை நெருங்குவதாக எடுத்துக் கொண்டால் ஹீரோனின் வாய்ப்பாடு கிடைக்கும். அதாவது ஒரு பக்கத்தின் நீளம் பூச்சியமாக உள்ள நாற்கரமாக முக்கோணத்தைக் கொள்ளலாம்.
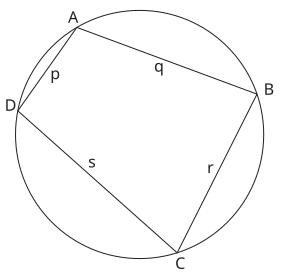
நிறுவல் [ தொகு ] இப்பகுதியின் நிறுவலுக்குப் பயன்படுத்தப்படும் வட்ட நாற்கரத்தின் படம். இப்பகுதியில் உள்ள படத்தில் தரப்பட்டுள்ள வட்ட நாற்கரத்தின் அளவுகளுக்கான குறியீடுகள் பரப்பு காணும்போது பயன்படுத்தப்படுகின்றன.
வட்ட நாற்கரம் ABCD -ன் பரப்பு
=
△
A
D
B
{\displaystyle =\triangle ADB}
△
B
D
C
{\displaystyle \triangle BDC}
=
1
2
p
q
sin
A
+
1
2
r
s
sin
C
.
{\displaystyle ={\frac {1}{2}}pq\sin A+{\frac {1}{2}}rs\sin C.}
A
B
C
D
{\displaystyle ABCD}
∠
D
A
B
=
180
∘
−
∠
D
C
B
.
{\displaystyle \angle DAB=180^{\circ }-\angle DCB.}
sin
A
=
sin
C
{\displaystyle \sin A=\sin C\,}
ஃ
Area
=
1
2
p
q
sin
A
+
1
2
r
s
sin
A
{\displaystyle {\mbox{Area}}={\frac {1}{2}}pq\sin A+{\frac {1}{2}}rs\sin A}
(
Area
)
=
1
2
sin
A
(
p
q
+
r
s
)
{\displaystyle ({\mbox{Area}})={\frac {1}{2}}\sin A(pq+rs)}
(
Area
)
2
=
1
4
sin
2
A
(
p
q
+
r
s
)
2
{\displaystyle ({\mbox{Area}})^{2}={\frac {1}{4}}\sin ^{2}A(pq+rs)^{2}}
4
(
Area
)
2
=
(
1
−
cos
2
A
)
(
p
q
+
r
s
)
2
=
(
p
q
+
r
s
)
2
−
cos
2
A
(
p
q
+
r
s
)
2
.
{\displaystyle 4({\mbox{Area}})^{2}=(1-\cos ^{2}A)(pq+rs)^{2}=(pq+rs)^{2}-\cos ^{2}A(pq+rs)^{2}.\,}
△
{\displaystyle \triangle }
ADB மற்றும்
△
{\displaystyle \triangle }
BDC , இரண்டின் பொதுப்பக்கம் DB-ன் மதிப்பைக் கொசைன் விதி மூலம் காண:
D
B
=
p
2
+
q
2
−
2
p
q
cos
A
=
r
2
+
s
2
−
2
r
s
cos
C
.
{\displaystyle DB=p^{2}+q^{2}-2pq\cos A=r^{2}+s^{2}-2rs\cos C.\,}
cos
C
=
cos
(
π
−
A
)
=
−
cos
A
{\displaystyle \cos C=\cos(\pi -A)=-\cos A\,}
A
{\displaystyle A}
C
{\displaystyle C}
மிகைநிரப்புக் கோணங்கள் .)இதனைப் பயன்படுத்த:
p
2
+
q
2
−
2
p
q
cos
A
=
r
2
+
s
2
+
2
r
s
cos
A
.
{\displaystyle p^{2}+q^{2}-2pq\cos A=r^{2}+s^{2}+2rs\cos A.\,}
உறுப்புகளை மாற்றித் தொகுக்க:
2
cos
A
(
p
q
+
r
s
)
=
p
2
+
q
2
−
r
2
−
s
2
.
{\displaystyle 2\cos A(pq+rs)=p^{2}+q^{2}-r^{2}-s^{2}.\,}
cos
A
(
p
q
+
r
s
)
=
p
2
+
q
2
−
r
2
−
s
2
2
.
{\displaystyle \cos A(pq+rs)={\frac {p^{2}+q^{2}-r^{2}-s^{2}}{2}}.\,}
வர்க்கப்படுத்த:
cos
2
A
(
p
q
+
r
s
)
2
=
(
p
2
+
q
2
−
r
2
−
s
2
)
2
4
.
{\displaystyle \cos ^{2}A(pq+rs)^{2}={\frac {(p^{2}+q^{2}-r^{2}-s^{2})^{2}}{4}}.\,}
இதனைப் பரப்பு வாய்ப்பாட்டில் பிரதியிட:
4
(
Area
)
2
=
(
p
q
+
r
s
)
2
−
1
4
(
p
2
+
q
2
−
r
2
−
s
2
)
2
{\displaystyle 4({\mbox{Area}})^{2}=(pq+rs)^{2}-{\frac {1}{4}}(p^{2}+q^{2}-r^{2}-s^{2})^{2}}
16
(
Area
)
2
=
4
(
p
q
+
r
s
)
2
−
(
p
2
+
q
2
−
r
2
−
s
2
)
2
,
{\displaystyle 16({\mbox{Area}})^{2}=4(pq+rs)^{2}-(p^{2}+q^{2}-r^{2}-s^{2})^{2},\,}
=
(
2
(
p
q
+
r
s
)
−
p
2
−
q
2
+
r
2
+
s
2
)
(
2
(
p
q
+
r
s
)
+
p
2
+
q
2
−
r
2
−
s
2
)
{\displaystyle =(2(pq+rs)-p^{2}-q^{2}+r^{2}+s^{2})(2(pq+rs)+p^{2}+q^{2}-r^{2}-s^{2})\,}
=
(
(
r
+
s
)
2
−
(
p
−
q
)
2
)
(
(
p
+
q
)
2
−
(
r
−
s
)
2
)
{\displaystyle =((r+s)^{2}-(p-q)^{2})((p+q)^{2}-(r-s)^{2})\,}
=
(
q
+
r
+
s
−
p
)
(
p
+
r
+
s
−
q
)
(
p
+
q
+
s
−
r
)
(
p
+
q
+
r
−
s
)
.
{\displaystyle =(q+r+s-p)(p+r+s-q)(p+q+s-r)(p+q+r-s).\,}
S
=
p
+
q
+
r
+
s
2
,
{\displaystyle S={\frac {p+q+r+s}{2}},}
16
(
Area
)
2
=
16
(
S
−
p
)
(
S
−
q
)
(
S
−
r
)
(
S
−
s
)
.
{\displaystyle 16({\mbox{Area}})^{2}=16(S-p)(S-q)(S-r)(S-s).\,}
(
Area
)
2
=
(
S
−
p
)
(
S
−
q
)
(
S
−
r
)
(
S
−
s
)
.
{\displaystyle ({\mbox{Area}})^{2}=(S-p)(S-q)(S-r)(S-s).\,}
வர்க்கமூலம் காண:
Area
=
(
S
−
p
)
(
S
−
q
)
(
S
−
r
)
(
S
−
s
)
.
{\displaystyle {\mbox{Area}}={\sqrt {(S-p)(S-q)(S-r)(S-s)}}.}
மாற்றுப் படிவம் [ தொகு ] இவ்வாய்ப்பாட்டின் மற்றொரு படிவம்:
K
=
(
a
2
+
b
2
+
c
2
+
d
2
)
2
+
8
a
b
c
d
−
2
(
a
4
+
b
4
+
c
4
+
d
4
)
4
⋅
{\displaystyle K={\frac {\sqrt {(a^{2}+b^{2}+c^{2}+d^{2})^{2}+8abcd-2(a^{4}+b^{4}+c^{4}+d^{4})}}{4}}\cdot }
நிறுவல் [ தொகு ] பரப்பு காணும் வாய்பாடின் பொதுப் படிவம்:
K
=
(
s
−
a
)
(
s
−
b
)
(
s
−
c
)
(
s
−
d
)
{\displaystyle K={\sqrt {(s-a)(s-b)(s-c)(s-d)}}}
s
−
a
=
−
a
+
b
+
c
+
d
2
{\displaystyle s-a={\frac {-a+b+c+d}{2}}}
s
−
b
=
a
−
b
+
c
+
d
2
{\displaystyle s-b={\frac {a-b+c+d}{2}}}
s
−
c
=
a
+
b
−
c
+
d
2
{\displaystyle s-c={\frac {a+b-c+d}{2}}}
s
−
d
=
a
+
b
+
c
−
d
2
{\displaystyle s-d={\frac {a+b+c-d}{2}}}
K
=
(
−
a
+
b
+
c
+
d
2
)
(
a
−
b
+
c
+
d
2
)
(
a
+
b
−
c
+
d
2
)
(
a
+
b
+
c
−
d
2
)
{\displaystyle K={\sqrt {({\frac {-a+b+c+d}{2}})({\frac {a-b+c+d}{2}})({\frac {a+b-c+d}{2}})({\frac {a+b+c-d}{2}})}}}
=
1
4
(
−
a
+
b
+
c
+
d
)
(
a
−
b
+
c
+
d
)
(
a
+
b
−
c
+
d
)
(
a
+
b
+
c
−
d
)
{\displaystyle ={\frac {1}{4}}{\sqrt {(-a+b+c+d)(a-b+c+d)(a+b-c+d)(a+b+c-d)}}}
=
1
4
[
(
c
+
d
)
−
(
a
−
b
)
]
[
(
c
+
d
)
+
(
a
−
b
)
]
[
(
a
+
b
)
−
(
c
−
d
)
]
[
(
a
+
b
)
+
(
c
−
d
)
]
{\displaystyle ={\frac {1}{4}}{\sqrt {[(c+d)-(a-b)][(c+d)+(a-b)][(a+b)-(c-d)][(a+b)+(c-d)]}}}
=
1
4
[
(
c
+
d
)
2
−
(
a
−
b
)
2
]
[
(
a
+
b
)
2
−
(
c
−
d
)
2
]
{\displaystyle ={\frac {1}{4}}{\sqrt {[(c+d)^{2}-(a-b)^{2}][(a+b)^{2}-(c-d)^{2}]}}}
=
1
4
[
(
c
2
+
d
2
−
a
2
−
b
2
+
2
a
b
+
2
c
d
]
[
(
a
2
+
b
2
−
c
2
−
d
2
+
2
a
b
+
2
c
d
]
{\displaystyle ={\frac {1}{4}}{\sqrt {[(c^{2}+d^{2}-a^{2}-b^{2}+2ab+2cd][(a^{2}+b^{2}-c^{2}-d^{2}+2ab+2cd]}}}
=
1
4
[
(
2
a
b
+
2
c
d
)
−
(
a
2
+
b
2
−
c
2
−
d
2
)
]
[
(
2
a
b
+
2
c
d
)
+
(
a
2
+
b
2
−
c
2
−
d
2
)
]
{\displaystyle ={\frac {1}{4}}{\sqrt {[(2ab+2cd)-(a^{2}+b^{2}-c^{2}-d^{2})][(2ab+2cd)+(a^{2}+b^{2}-c^{2}-d^{2})]}}}
=
1
4
(
2
a
b
+
2
c
d
)
2
−
(
a
2
+
b
2
−
c
2
−
d
2
)
2
{\displaystyle ={\frac {1}{4}}{\sqrt {(2ab+2cd)^{2}-(a^{2}+b^{2}-c^{2}-d^{2})^{2}}}}
=
1
4
[
(
4
a
2
b
2
+
4
c
2
d
2
+
8
a
b
c
d
)
−
(
a
4
+
b
4
+
c
4
+
d
4
+
2
a
2
b
2
−
2
a
2
c
2
−
2
a
2
d
2
−
2
b
2
c
2
−
2
b
2
d
2
+
2
c
2
d
2
)
{\displaystyle ={\frac {1}{4}}{\sqrt {[(4a^{2}b^{2}+4c^{2}d^{2}+8abcd)-(a^{4}+b^{4}+c^{4}+d^{4}+2a^{2}b^{2}-2a^{2}c^{2}-2a^{2}d^{2}-2b^{2}c^{2}-2b^{2}d^{2}+2c^{2}d^{2})}}}
=
1
4
(
2
a
2
b
2
+
2
a
2
c
2
+
2
a
2
d
2
+
2
b
2
c
2
+
2
b
2
d
2
+
2
c
2
d
2
)
+
8
a
b
c
d
−
(
a
4
+
b
4
+
c
4
+
d
4
)
{\displaystyle ={\frac {1}{4}}{\sqrt {(2a^{2}b^{2}+2a^{2}c^{2}+2a^{2}d^{2}+2b^{2}c^{2}+2b^{2}d^{2}+2c^{2}d^{2})+8abcd-(a^{4}+b^{4}+c^{4}+d^{4})}}}
=
1
4
(
a
2
+
b
2
+
c
2
+
d
2
)
2
−
(
a
4
+
b
4
+
c
4
+
d
4
)
+
8
a
b
c
d
−
(
a
4
+
b
4
+
c
4
+
d
4
)
{\displaystyle ={\frac {1}{4}}{\sqrt {(a^{2}+b^{2}+c^{2}+d^{2})^{2}-(a^{4}+b^{4}+c^{4}+d^{4})+8abcd-(a^{4}+b^{4}+c^{4}+d^{4})}}}
=
1
4
(
a
2
+
b
2
+
c
2
+
d
2
)
2
+
8
a
b
c
d
−
2
(
a
4
+
b
4
+
c
4
+
d
4
)
{\displaystyle ={\frac {1}{4}}{\sqrt {(a^{2}+b^{2}+c^{2}+d^{2})^{2}+8abcd-2(a^{4}+b^{4}+c^{4}+d^{4})}}}
வட்டத்துக்குள் அமையாத நாற்கரங்களுக்கு நீட்டிப்பு [ தொகு ] வட்டத்துக்குள் அமையாத நாற்கரங்களின் பரப்பு காண்பதற்கு பிரம்மகுப்தரின் வாய்ப்பாட்டை நீட்டித்துக் கொள்ளலாம். இதற்கு நாற்கரங்களின் எதிர்க் கோணங்களின் அளவுகளைக் கருத்தில் கொள்ளல் வேண்டும்.
K
=
(
s
−
a
)
(
s
−
b
)
(
s
−
c
)
(
s
−
d
)
−
a
b
c
d
cos
2
θ
{\displaystyle K={\sqrt {(s-a)(s-b)(s-c)(s-d)-abcd\cos ^{2}\theta }}}
பிரெட்ஷ்னீடரின் வாய்ப்பாடாகும். இங்கு θ, நாற்கரத்தின் ஏதேனும் ஒரு சோடி எதிர்க் கோணங்களின் கூட்டுத்தொகையில் பாதி. இரண்டு சோடி எதிர்க் கோணங்களில் எந்த சோடியை வேண்டுமானாலும் எடுத்துக் கொள்ளலாம். ஏனெனில் மற்றொரு சோடி எதிர்க்கோணங்களின் கூட்டுத்தொகையில் பாதியானது, (180- θ) -ஆக இருக்கும். cos(180° − θ) = −cosθ, cos2 (180° − θ) = cos2 θ.
தரப்பட்ட பக்க நீளங்களைக் கொண்ட நாற்கரங்களிலேயே வட்ட நாற்கரங்கள் தான் மீப்பெரு பரப்புடையவை.
பொது நாற்கரங்களின் பரப்பு வாய்ப்பாட்டிலிருந்து வட்ட நாற்கரங்களின் பரப்பு காணும் வாய்ப்பாட்டைப் பெறுதல்:
வட்ட நாற்கரங்களின் பண்பின்படி அதன் எதிர்க் கோணங்கள் மிகைநிரப்புக் கோணங்கள். எனவே அவற்றின் கூடுதல் 180°, இக்கூடுதலின் பாதியளவு 90°
ஃ
a
b
c
d
cos
2
θ
=
a
b
c
d
cos
2
(
90
∘
)
=
a
b
c
d
⋅
0
=
0
,
{\displaystyle abcd\cos ^{2}\theta =abcd\cos ^{2}\left(90^{\circ }\right)=abcd\cdot 0=0,\,}
எனவே பரப்பு வாய்ப்பாட்டில் இதைப் பிரதியிட வட்ட நாற்கரத்தின் பரப்பு காணும் பிரம்மகுப்தரின் வாய்ப்பாடு கிடைக்கிறது:
K
=
(
s
−
a
)
(
s
−
b
)
(
s
−
c
)
(
s
−
d
)
{\displaystyle K={\sqrt {(s-a)(s-b)(s-c)(s-d)}}}
ஜூலியன் கூலிட்ஜ் -ஆல் நிறுவப்பட்ட பொதுக் குவிவு நாற்கரங்களின் பரப்பு காணும் வாய்ப்பாடு:[1]
K
=
(
s
−
a
)
(
s
−
b
)
(
s
−
c
)
(
s
−
d
)
−
1
4
(
a
c
+
b
d
+
p
q
)
(
a
c
+
b
d
−
p
q
)
{\displaystyle K={\sqrt {(s-a)(s-b)(s-c)(s-d)-\textstyle {1 \over 4}(ac+bd+pq)(ac+bd-pq)}}\,}
இங்கு p மற்றும் q -நாற்கரத்தின் மூலைவிட்டங்களின் நீளங்கள்.
டாலமியின் தேற்றப்படி , ஒரு வட்ட நாற்கரத்திற்கு,
p
q
=
a
c
+
b
d
{\displaystyle pq=ac+bd}
தொடர்புள்ள பிற தேற்றங்கள் [ தொகு ] முக்கோணங்களின் பரப்பு காணும் ஹீரோனின் வாய்ப்பாடு - நாற்கரத்தின் பக்க நீளம் d = 0 எனக் கொள்வதால் கிடைக்கும் சிறப்பு வகை.
பிரம்மகுப்தரின் பொது வாய்ப்பாட்டிற்கும் நீட்டிக்கப்பட்ட வாய்ப்பாட்டிற்கும் உள்ள தொடர்பு, கொசைன் விதியானது பித்தகோரஸ் தேற்றத்தின் நீட்டிப்பாக அமைதலுக்குச் சமமானது. வெளி இணைப்புகள் [ தொகு ] மேற்கோள்கள் [ தொகு ]
↑ J. L. Coolidge, "A Historically Interesting Formula for the Area of a Quadrilateral", American Mathematical Monthly , 46 (1939) pp. 345-347.
This article incorporates material from ப்ளேனட் மேத் தளத்தில் proof of Brahmagupta's formula , which is licensed under the Creative Commons Attribution/Share-Alike License.






































![{\displaystyle ={\frac {1}{4}}{\sqrt {[(c+d)-(a-b)][(c+d)+(a-b)][(a+b)-(c-d)][(a+b)+(c-d)]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0554cfe6eeacbd25f68ad080c582415f539dcee2)
![{\displaystyle ={\frac {1}{4}}{\sqrt {[(c+d)^{2}-(a-b)^{2}][(a+b)^{2}-(c-d)^{2}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9bcbf317609b2f1a7f0cc3e3f43fb359b114336c)
![{\displaystyle ={\frac {1}{4}}{\sqrt {[(c^{2}+d^{2}-a^{2}-b^{2}+2ab+2cd][(a^{2}+b^{2}-c^{2}-d^{2}+2ab+2cd]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/267be92641b494694f92419335699dccd76971ae)
![{\displaystyle ={\frac {1}{4}}{\sqrt {[(2ab+2cd)-(a^{2}+b^{2}-c^{2}-d^{2})][(2ab+2cd)+(a^{2}+b^{2}-c^{2}-d^{2})]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/abc7c0d74210f9d2a63fb680081848f086b25d9b)








