தொடுகோட்டு நாற்கரம்

நாற்கரம் அல்லது நாற்கோணம் ஒன்றின் நான்கு பக்கங்களும், அந்த நாற்கரத்தின் உள்ளே வரையப்பட்ட வட்டம் ஒன்றுக்குத் தொடுகோடுகளாக அமையும் என்றால் அந்த நாற்கரம் தொடுகோட்டு நாற்கரம் அல்லது தொடுநாற்கரம் (Tangential quadrilateral) எனப்படும். இந்த வட்டமானது நாற்கரத்தின் உள்வட்டம் என்றும் அதன் மையம் உள்வட்டமையம் என்றும் ஆரம் உள்வட்ட ஆரம் எனவும் அழைக்கப்படுகின்றன. தொடு பல்கோணங்களின் ஒரு வகையாகத் தொடுநாற்கரங்கள் அமையும்.

எல்லா முக்கோணங்களுக்கும் உள்வட்டம் உண்டு. ஆனால் எல்லா நாற்கரங்களுக்கும் உள்வட்டம் இருக்காது. எடுத்துக்காட்டாக, செவ்வகத்திற்கு உள்வட்டம் கிடையாது. அதாவது செவ்வகம் ஒரு தொடுநாற்கரமல்ல.

சிறப்பு வகைகள்[தொகு]

தொடு நாற்கரங்களுக்கான எடுத்து பட்டங்கள் தொடு நாற்கரங்களாகும். சாய்சதுரங்கள் பட்டங்களுக்குள் அடங்குவதால் அவையும் தொடுநாற்கரங்கள். சதுரங்கள், சாய்சதுரங்களுக்குள் அடங்கும் என்பதால் சதுரங்களும் தொடுநாற்கரங்கள். சதுரம். பட்டங்கள், செங்குத்து மூலைவிட்ட நாற்கரங்களாகவுமுள்ள தொடுநாற்கரங்கள்.^[1] ஒரு செங்கோணப் பட்டத்துக்குச் சுற்றுவட்டமும் உண்டு என்பதால் அது தொடுநாற்கரமாகவும் வட்டநாற்கரமாகவும் இருக்கும். தொடுநாற்கரமாகவும் வட்டநாற்கரமாகவுமுள்ள நாற்கரங்கள் இருமைய நாற்கரங்கள் எனப்படும். தொடு நாற்கரமாகவும் சரிவகமாகவுமுள்ள நாற்கரம், தொடு சரிவகம் எனப்படும்.

பண்பாக்கங்கள்[தொகு]

ஒரு தொடுநாற்கரத்தின் நான்கு கோண இருசமவெட்டிகளும் உள்வட்ட மையத்தில் சந்திக்கும். மறுதலையாக, ஒரு குவிவு நாற்கரத்தின் நான்கு கோண இருசமவெட்டிகளும் ஒரு புள்ளியில் சந்தித்தால் அந்த நாற்கரம் தொடுநாற்கரமாக இருக்கும். மேலும், அந்த சந்திக்கும் புள்ளி நாற்கரத்தின் உள்வட்ட மையமாக இருக்கும்.^[2]

பீட்டோ தேற்றத்தின்படி, ஒரு தொடுநாற்கரத்தின் இரு சோடி எதிர்பக்கங்களின் நீளங்களின் கூடுதல் சமமாகவும் நாற்கரத்தின் அரைச்சுற்றளவாகவும் (s) இருக்கும்:

a+c=b+d={\frac {a+b+c+d}{2}}=s.

(நாற்கரத்தின் பக்கங்கள்: a, b c, d)

மறுதலையாக, ஒரு குவிவு நாற்கரத்தில் a + c = b + d ஆக இருந்தால் அந்நாற்கரம் கண்டிப்பாகத் தொடுநாற்கரமாகும்.^[3]^:p.65^[2]

குவிவு நாற்கரம் ABCD (சரிவகமற்ற) இன் எதிர்பக்கங்கள் வெட்டும் புள்ளிகள் E, F எனில்:^[2]

\displaystyle BE+BF=DE+DF

அல்லது

\displaystyle AE-EC=AF-FC.

என இருந்தால், இருந்தால் மட்டுமே, அந்நாற்கரம் தொடுநாற்கரமாக முடியும்.

இரண்டாவது முடிவு கிட்டத்தட்ட உர்க்கார்ட்டின் தேற்றத்தின் சமனிகளுள் ஒன்றாகும். இருபுறமுமுள்ள குறிகள் மட்டுமே வேறுபடுகின்றன. இரண்டாவது முடிவில் வித்தியாசங்களும், உர்க்கார்ட்டின் தேற்ற முடிவில் கூடுதல்களும் எடுத்துக்கொள்ளப்பட்டுள்ளன.

ABCD நாற்கரம் ஒரு தொடுநாற்கரமாக இருப்பதற்கான மற்றுமொரு தேவையானதும் போதுமானதுமான கட்டுப்பாடு: ABC, ADC ஆகிய இரு முக்கோணங்களின் உள்வட்டங்கள் இரண்டும் ஒன்றையொன்று தொடும் வட்டங்களாக இருக்க வேண்டும்.^[3]^:p.66

$\tan {\frac {\angle ABD}{2}}\cdot \tan {\frac {\angle BDC}{2}}=\tan {\frac {\angle ADB}{2}}\cdot \tan {\frac {\angle DBC}{2}}.$ என இருந்தால், இருந்தால் மட்டுமே, குவிவு நாற்கரம் ABCD ஒரு தொடுநாற்கரமாகும்.^[4]

$R_{a}R_{c}=R_{b}R_{d}$ என இருந்தால், இருந்தால் மட்டுமே, a, b, c, d ஐ தொடர் பக்கங்களாக்கொண்ட குவிவு நாற்கரம் தொடுநாற்கரமாக இருக்கும். இதிலுள்ள R_a, R_b, R_c, R_d என்பவை a, b, c, d பக்கங்கள் ஒவ்வொன்றையும், அவற்றின் இரு அயல்பக்கங்களின் நீட்சிகளையும் வெளிப்பக்கமாகத் தொடும் வட்டங்களின் ஆரங்கள்.^[5]^:p.72

சிறப்பு கோட்டுத்துண்டுகள்[தொகு]

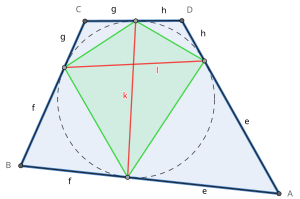
தொடுநாற்கரத்தின் உள்வட்டத்திற்கு எட்டு தொடுகோட்டுத் துண்டுகள் உள்ளன. தொடுநாற்கரத்தின் ஒவ்வொரு உச்சியையும் அந்த உச்சியைப் பொதுப்புள்ளியாகக் கொண்ட இரு பக்கங்களை உள்வட்டம் தொடும் புள்ளிகளையும் இணைக்கும் கோட்டுத்துண்டுகளே தொடுகோட்டுத்துண்டுகளாகும். (e, f, g, h ) ஆகும். ஒவ்வொரு உச்சியிலிருந்தும் அமையும் இரு தொடுகோடுகளும் முற்றொத்தவை (சமநீளமுள்ளவை).

தொடுநாற்கரத்தின் எதிரெதிர் பக்கங்களிலுள்ள தொடுபுள்ளிகளை இணைக்கும் கோட்டுத்துண்டுகள் தொடுநிலை நாண்களாகும் (படத்தில் k, l). நான்கு தொடுபுள்ளிகளால் அமையும் நாற்கரத்தின் மூலைவிட்டங்களாக இந்நாண்கள் அமையும்.

பரப்பளவு[தொகு]

முக்கோணவியலற்ற வாய்பாடுகள்[தொகு]

தொடுநாற்கரத்தின் பரப்பளவு (K):

$\displaystyle K=r\cdot s,$ s - அரைச்சுற்றளவு; r - உள்வட்ட ஆரம்.
$\displaystyle K={\tfrac {1}{2}}{\sqrt {p^{2}q^{2}-(ac-bd)^{2}}}$ ^[6] p, q மூலைவிட்டங்கள்; a, b, c, d பக்கங்கள்.
$\displaystyle K={\sqrt {(e+f+g+h)(efg+fgh+ghe+hef)}},$ தொடுகோட்டு நீளங்கள் e, f, g, h.^[1]
$K={\sqrt {abcd-(eg-fh)^{2}}},$ பக்கங்கள் a, b, c, d, தொடுகோட்டு நீளங்கள் e, f, g, h ^[1]^:p.128

இருமைய நாற்கரங்களாக இருந்தால், இருந்தால் மட்டுமே eg = fh ஆக இருக்கும் என்பதால், தொடுநாற்கரம் ஒரு இருமைய நாற்கரமாக இருந்தால் மட்டுமே, அதன் பரப்பளவு மிகப்பெரியளவாக இருக்கும்.^[7] பெருமப் பரப்பளவு:

{\sqrt {abcd}}

முக்கோணவியல் வாய்பாடுகள்[தொகு]

\displaystyle K={\sqrt {abcd}}\sin {\frac {A+C}{2}}={\sqrt {abcd}}\sin {\frac {B+D}{2}}.

பக்கங்கள் a, b, c, d; கோணங்கள்: A, B, C, D^[6]^[8]^[9]^[10]

தொடுநாற்கரம் ஒரு இருமைய நாற்கரமாக இருந்தால் மட்டுமே, அதன் பரப்பளவு மிகப்பெரியளவாக இருக்கும். மேலும், இருமைய நாற்கரம் ஒரு வட்டநாற்கரமுங்கூட என்பதால் எதிர்கோணங்களின் கூடுதல் 180°. எனவே பெருமப் பரப்பளவு: $K={\sqrt {abcd}}$

$K=\left(IA\cdot IC+IB\cdot ID\right)\sin {\frac {A+C}{2}}$ ^[9]^:p.19, உள்வட்ட மையம்: I..
$K=ab\sin {\frac {B}{2}}\csc {\frac {D}{2}}\sin {\frac {B+D}{2}}.$ ^[6]
$K={\tfrac {1}{2}}|(ac-bd)\tan {\theta }|,$ ^[6] இரு மூலைவிட்டங்களுக்கு இடைப்பட்ட ஒரு கோணம் θ. பட்டங்களில் θ = 90° ஆக இருக்கும் என்பதால் இவ்வாய்பாடு பட்டங்களுக்குப் பொருந்தாது.

சமனிலிகள்[தொகு]

$K\leq {\sqrt {abcd}},$ தொடுநாற்கரத்தின் பக்கங்கள் a, b, c, d. இருமைய நாற்கரங்களுக்கு மட்டுமே சமக்குறி பொருந்தும்.

அரைச்சுற்றளவு s; உள்வட்ட ஆரம் r எனில் $s\geq 4r.$ (சதுரங்களுக்கு மட்டுமே சமக்குறி பொருந்தும்)^[11] இதனைத் தொடுநாற்கரத்தின் பரப்பளவு வாய்பாடு K = rs இல் பயன்படுத்தக் கிடைக்கும் சமனிலி

K\geq 4r^{2}

(சதுரத்துக்கு மட்டுமே சமக்குறி பொருந்தும்)

பிரிப்பு பண்புகள்[தொகு]

உள்வட்ட மையத்தையும், உள்வட்டம் தொடுநாற்கரத்தின் பக்கங்களைத் தொடும்புள்ளிகளையும் இணைக்கும் நான்கு கோட்டுத்துண்டுகளும் நாற்கரத்தை நான்கு நேர் பட்டங்களாகப் பிரிக்கும்.
தொடு நாற்கரத்தை சமபரப்பளவும் சம சுற்றளவுமுள்ள இரு பல்கோணங்களாகப் பிரிக்கும் கோடு உள்வட்ட மையத்தின் வழியாகச் செல்லும்.^[2]

உள்வட்ட ஆரம்[தொகு]

தொடர்ச்சியான பக்கங்கள் a, b, c, d கொண்ட தொடுநாற்கரத்தின் உள்வட்ட ஆரத்திற்கான வாய்பாடு:^[6]

$r={\frac {K}{s}}={\frac {K}{a+c}}={\frac {K}{b+d}},$ பரப்பளவு K; அரைச்சுற்றளவு s. இருமைய நாற்கரமாக இருக்கும்போது உள்வட்ட ஆரம் பெரும மதிப்பு கொண்டிருக்கும்.
$\displaystyle r={\sqrt {\frac {efg+fgh+ghe+hef}{e+f+g+h}}},$ தொடுகோட்டு நீளங்கள் e, f, g, h.^[7]^:Lemma2^[12]
நாற்கரம் ABCD இன் உள்வட்டமையம் I; u = AI, v = BI, x = CI, y = DI எனில்:

r=2{\sqrt {\frac {(\sigma -uvx)(\sigma -vxy)(\sigma -xyu)(\sigma -yuv)}{uvxy(uv+xy)(ux+vy)(uy+vx)}}},

\sigma ={\tfrac {1}{2}}(uvx+vxy+xyu+yuv)

.^[13]

ABC, BCD, CDA, DAB முக்கோணங்களின் உள்வட்ட ஆரங்கள் முறையே $r_{1},r_{2},r_{3},r_{4}$ எனில்:

r={\frac {G+{\sqrt {G^{2}-4r_{1}r_{2}r_{3}r_{4}(r_{1}r_{3}+r_{2}r_{4})}}}{2(r_{1}r_{3}+r_{2}r_{4})}},

G=r_{1}r_{2}r_{3}+r_{2}r_{3}r_{4}+r_{3}r_{4}r_{1}+r_{4}r_{1}r_{2}

.^[14]

கோணங்களின் வாய்பாடு[தொகு]

தொடு நாற்கரம் ABCD இன் உச்சிகள் A, B, C, D களிலிருந்து உள்வட்டத்துக்குத் தொடுகோட்டு நீளங்கள் முறையே e, f, g, h எனில் நாற்கரத்தின் கோணங்களின் வாய்பாடுகள்:^[1]

\sin {\frac {A}{2}}={\sqrt {\frac {efg+fgh+ghe+hef}{(e+f)(e+g)(e+h)}}},

\sin {\frac {B}{2}}={\sqrt {\frac {efg+fgh+ghe+hef}{(f+e)(f+g)(f+h)}}},

\sin {\frac {C}{2}}={\sqrt {\frac {efg+fgh+ghe+hef}{(g+e)(g+f)(g+h)}}},

\sin {\frac {D}{2}}={\sqrt {\frac {efg+fgh+ghe+hef}{(h+e)(h+f)(h+g)}}}.

தொடுநிலை நாண்கள் k, l இரண்டுக்கும் இடைப்பட்ட கோணம்:^[1]

\sin {\varphi }={\sqrt {\frac {(e+f+g+h)(efg+fgh+ghe+hef)}{(e+f)(f+g)(g+h)(h+e)}}}.

மூலைவிட்டங்கள்[தொகு]

தொடுகோட்டு நீளங்கள் e, f, g, h எனில், மூலைவிட்டங்களின் நீளங்கள் p = AC, q = BD இன் மதிப்புகள்:^[7]^:Lemma3

\displaystyle p={\sqrt {{\frac {e+g}{f+h}}{\Big (}(e+g)(f+h)+4fh{\Big )}}},

\displaystyle q={\sqrt {{\frac {f+h}{e+g}}{\Big (}(e+g)(f+h)+4eg{\Big )}}}.

தொடுநிலை நாண்கள்[தொகு]

தொடுநாற்கரத்தின் தொடுகோட்டு நீளங்கள் e, f, g, h எனில், அதன் தொடுநிலை நாண்களின் நீளங்கள்:^[1]

\displaystyle k={\frac {2(efg+fgh+ghe+hef)}{\sqrt {(e+f)(g+h)(e+g)(f+h)}}},

\displaystyle l={\frac {2(efg+fgh+ghe+hef)}{\sqrt {(e+h)(f+g)(e+g)(f+h)}}}

இதில், தொடுநாற்கரத்தின் a = e + f, c = g + h பக்கங்களை இணைக்கும் நாண் k; b = f + g, d = h + e பக்கங்களை இணைக்கும் நாண் l.

தொடுநிலை நாண்களின் வர்க்கங்களின் விகிதங்கள் பின்னுள்ளவாறு அமையும்:^[1]

{\frac {k^{2}}{l^{2}}}={\frac {bd}{ac}}.

தொடுநாற்கரத்துக்கு சுற்றுவட்டம் இருந்தால், இருந்தால் மட்டுமே (இருமைய நாற்கரமாக) அதன் தொடுநிலை நாண்கள் ஒன்றுக்கொன்று செங்குத்தானவை.^[1]^:p.124

தொடுநாற்கரம் ஒரு பட்டமாக இருந்தால், இருந்தால் மட்டுமே அதன் தொடுநிலை நாண்கள் சமநீளமுள்ளவை.^[15]^:p.166

தொடுநாற்கரம் ABCD இன் AB, CD பக்கங்களுக்கு இடையேயுள்ள இருநடுக்கோட்டைவிட, BC, DA பக்கங்களுக்கு இடையேயுள்ள இருநடுக்கோடு நீளமானதாக இருந்தால், இருந்தால் மட்டுமே, AB, CD பக்கங்களுக்கு இடையேயுள்ள தொடுநிலை நாணானது BC, DA பக்கங்களுக்கு இடைப்பட்ட தொடுநிலை நாணைவிட நீளமானது.^[16]^:p.162

தொடு நாற்கரம் ABCD இல் AB பக்கத்தின் தொடுநிலை புள்ளி W; CD பக்கத்தின் மீதான தொடுநிலை புள்ளி Y. மேலும் WY நாண், BD மூலைவிட்டத்தைச் சந்திக்கும் புள்ளி M எனில்:

{\tfrac {BW}{DY}}={\tfrac {BM}{DM}}

^[17]

ஒருகோட்டுப் புள்ளிகள்[தொகு]

தொடுநாற்கரம் ABCD இன் மூலைவிட்டங்கள் AC, BD இன் நடுப்புள்ளிகள் முறையே M₁, M₂; உள்வட்டமையம் I; எதிர்பக்க சோடிகள் சந்திக்கும் புள்ளிகள் J, K; JK இன் நடுப்புள்ளி M₃ எனில், M₃, M₁, I, M₂ ஆகிய நான்கு புள்ளிகளும் ஒரே கோட்டின் மீதமையும்.^[2]^:p.42 அவை அமையும் கோடு, தொடுநாற்கரத்தின் நியூட்டன் கோடு ஆகும்.

தொடுநாற்கரத்தின் எதிர்பக்கங்களின் நீட்சிகள் J, K புள்ளிகளிலும், தொடுநிலை புள்ளிகளாலான நாற்கரத்தின் எதிர்பக்கங்களின் நீட்சிகள் L, M புள்ளிகளிலும் சந்தித்தால், J, L, K',' M நான்கும் ஒருகோட்டுப் புள்ளிகள்^[18]^:Cor.3

தொடுநாற்கரத்தின் AB, BC, CD, DA பக்கங்களை உள்வட்டம் தொடும்புள்ளிகள் முறையே T₁, T₂, T₃, T₄. மேலும் இப்புள்ளிகளின் சமவியல்பு இணையியங்கள் முறையே N₁, N₂, N₃, N₄ (அதாவது, AT₁ = BN₁ ...) எனில், N₁N₃, N₂N₄. கோடுகள் வெட்டிக்கொள்ளும் புள்ளியானது தொடுநாற்கரத்தின் நாகெல் புள்ளியென வரையறுக்கப்படுகிறது. இவ்விரு கோடுகளும் நாற்கரத்தின் சுற்றளவை இரு சமபாகங்களாகப் பிரிக்கின்றன.நாகெல் புள்ளி N, நாற்கரத்தின் பரப்பளவு திணிவுமையம் G, உள்வட்டமையம் I மூன்றும் இதே வரிசையில் ஒரே கோட்டிலமையும். மேலும் NG = 2GI. இக்கோடு தொடுநாற்கரத்தின் நாகெல் கோடு எனப்படும்.^[19]

தொடுநாற்கரம் ABCD இன் உள்வட்டமையம் I. அதன் மூலைவிட்டங்கள் வெட்டும் புள்ளி P. AIB, BIC, CID, DIA முக்கோணங்களின் செங்குத்து மையங்கள் H_X, H_Y, H_Z, H_W எனில், P, H_X, H_Y, H_Z, H_W நேர்கோட்டிலமையும்.^[9]^:p.28

ஒருபுள்ளியில் சந்திக்கும் கோடுகளும் செங்குத்துக்கோடுகளும்[தொகு]

தொடுநாற்கரத்தின் இரு மூலைவிட்டங்களும் இரு தொடுநிலை நாண்களும் ஒருபுள்ளியில் சந்திக்கும் கோடுகள்.^[10]^[9]^:p.11

தொடுநாற்கரத்தின் எதிர்பக்கங்களின் நீட்சிகள் J, K புள்ளிகளிலும் மூலைவிட்டங்கள் P இலும் சந்தித்தால், JK, IP இன் நீட்சிக்குச் செங்குத்தானது (I உள்வட்டமையம்).^[18]^:Cor.4

உள்வட்ட மையம்[தொகு]

தொடுநாற்கரத்தின் மூலைவிட்டங்களின் நடுப்புள்ளிகளை இணைக்கும் நியூட்டன் கோட்டின்மீது உள்வட்டமையம் அமையும்.^[20]^{:Thm. 3}

தொடுநாற்கரத்தின் எதிர்பக்கங்களின் விகிதத்தை அதன் உச்சிகளுக்கும் உள்வட்டமையத்துக்கும் இடைப்பட்ட தூரங்களின் வாயிலாக எழுதலாம்:^[9]^:p.15

{\frac {AB}{CD}}={\frac {IA\cdot IB}{IC\cdot ID}},\quad \quad {\frac {BC}{DA}}={\frac {IB\cdot IC}{ID\cdot IA}}.

தொடுநாற்கரம் ABCD இன் அடுத்துள்ள பக்கநீளங்களின் பெருக்குத்தொகை:^[21]

AB\cdot BC=IB^{2}+{\frac {IA\cdot IB\cdot IC}{ID}}.

தொடுநாற்கரம் ABCD இல்^[9]^:p.16

IA\cdot IC+IB\cdot ID={\sqrt {AB\cdot BC\cdot CD\cdot DA}}.

The incenter I in a tangential quadrilateral தொடுநாற்கரம் ABCD இன் உச்சி திணிவுமையத்துடன் உள்வட்டமையம் ஒன்றுபடுவதற்குத் தேவையானதும் போதுமானதுமான கட்டுப்பாடு:^[9]^:p.22

IA\cdot IC=IB\cdot ID.

AC, BD மூலைவிட்டங்களின் நடுப்புள்ளிகள் முறையே M_p and M_q எனில்:^[9]^:p.19^[22]

{\frac {IM_{p}}{IM_{q}}}={\frac {IA\cdot IC}{IB\cdot ID}}={\frac {e+g}{f+h}}

A, B, C, D உச்சிகளிலிருந்தமையும் தொடுகோட்டு நீளங்கள் முறையே e, f, g, h.

ஒரு நான்கு தண்டு இயங்கமைவு தொடுநாற்கர வடிவிலமைக்கப்பட்டிருந்தால், இணைப்புகளை நெகிழ்த்தினாலும் குவிந்ததாக இருக்கும்வரை தொடுநாற்கரமாகவே இருக்கும்.^[23]^[24] (எடுத்துக்காட்டாக, ஒரு சதுரத்தின் வடிவை சாய்சதுரமாக்கினாலும் தொடுவட்டம் சிறிதாவதைத் தவிர,அதன் தொடுநாற்கரத்தன்மை மாறுவதில்லை). ஒரு பக்கத்தை நிலையாக வைத்துக்கொண்டு நாற்கரத்தை நெகிழ்த்தும்போது அதன் உள்வட்டமைய வழிப்பாதை ${\sqrt {abcd}}/s$ ஆரமுள்ள ஒரு வட்டமாக இருக்கும். இதில் a, b, c, d நாற்கரத்தின் தொடர்பக்கங்கள்; s அரைச்சுற்றளவு.

நான்கு உள்முக்கோணங்களில் பண்பாக்கங்கள்[தொகு]

குவிவு நாற்கரம் ABCD இன் முக்கோணங்கள் P புள்ளியில் வெட்டிக்கொள்கின்றன. இதனால் நாற்கரம் ஒன்றுக்கொன்று பொதுப்பகுதிகள் இல்லாத APB, BPC, CPD, DPA ஆகிய நான்கு முக்கோணங்களாகப் பிரிக்கப்படுகிறது. இந்நாற்கரம் தொடுநாற்கரமாக அமைவதற்கான பண்பாக்கங்கள்:

APB, BPC, CPD, DPA முக்கோணங்களின் உள்வட்ட ஆரங்கள் முறையே r₁, r₂, r₃, r₄ எனில் கீழுள்ள முடிவு உண்மையாக இருந்தால், இருந்தால் மட்டுமே, தொடுநாற்கரமாக இருக்கும்:^[25]

{\frac {1}{r_{1}}}+{\frac {1}{r_{3}}}={\frac {1}{r_{2}}}+{\frac {1}{r_{4}}}.

^[15]^:p.169^[26]

மேலே தரபட்ட அதே நான்கு முக்கோணங்களின் குத்துக்கோடுகள் h₁, h₂, h₃, h₄ எனில் கீழேயுள்ள முடிவு உண்மையாக இருந்தால், இருந்தால் மட்டுமே, தொடுநாற்கரமாக இருக்க முடியும்.^[4]^[26]

{\frac {1}{h_{1}}}+{\frac {1}{h_{3}}}={\frac {1}{h_{2}}}+{\frac {1}{h_{4}}}.

அந்நான்கு முக்கோணங்களின் வெளிவட்ட ஆரங்கள் முறையே r_a, r_b, r_c, r_d எனில் பின்வரும் முடிவு உண்மையாக இருந்தால், இருந்தால் மட்டுமே, தொடுநாற்கரமாகும்.^[3]^:p.70

{\frac {1}{r_{a}}}+{\frac {1}{r_{c}}}={\frac {1}{r_{b}}}+{\frac {1}{r_{d}}}.

APB, BPC, CPD, DPA முக்கோணங்களின் சுற்றுவட்ட ஆரங்கள் முறையே R₁, R₂, R₃, R₄ எனில் கீழுள்ள முடிவு உண்மையாக இருந்தால், இருந்தால் மட்டுமே, நாற்கரம் ABCD, தொடுநாற்கரமாகும்^[27]^{:pp. 23–24}

R_{1}+R_{3}=R_{2}+R_{4}.

APB, BPC, CPD, DPA முக்கோணங்களின் உள்வட்ட மையங்கள் ஒரு வட்டநாற்கரத்தை (செங்குத்து மூலைவிட்ட வட்ட நாற்கரம்) அமைத்தால், அமைத்தால் மட்டுமே நாற்கரம் தொடுநாற்கரமாக இருக்கும்.^[3]^{:pp. 72–73}^[3]^:p.74 இதேபோல மேலுள்ள நான்கு முக்கோணங்களின் வெளிவட்ட மையங்கள் ஒரு வட்ட நாற்கரத்தின் உச்சிகளாக இருந்தால், இருந்தால் மட்டுமே, நாற்கரம் தொடுநாற்கரமாக இருக்கும்.^[3]^{:p. 73}

தொடுநாற்கரமாக இருப்பதற்கான மற்றுமொரு தேவையானதும் போதுமானதுமான கட்டுப்பாடு:^[4]

{\frac {a}{\triangle (APB)}}+{\frac {c}{\triangle (CPD)}}={\frac {b}{\triangle (BPC)}}+{\frac {d}{\triangle (DPA)}},

இதில் ∆(APB) = முக்கோணம் APB இன் பரப்பளவு.

AP = p₁, PC = p₂, BP = q₁, PD = q₂ எனில், பின்வரும் முடிவு உண்மையாக இருந்தால், இருந்தால் மட்டுமே தொடுநாற்கரமாகும்:^[28]

ap_{2}q_{2}+cp_{1}q_{1}=bp_{1}q_{2}+dp_{2}q_{1}

(அல்லது)

{\frac {(p_{1}+q_{1}-a)(p_{2}+q_{2}-c)}{(p_{1}+q_{1}+a)(p_{2}+q_{2}+c)}}={\frac {(p_{2}+q_{1}-b)(p_{1}+q_{2}-d)}{(p_{2}+q_{1}+b)(p_{1}+q_{2}+d)}}

^[3]^{:p. 74}

(அல்லது)

{\frac {(a+p_{1}-q_{1})(c+p_{2}-q_{2})}{(a-p_{1}+q_{1})(c-p_{2}+q_{2})}}={\frac {(b+p_{2}-q_{1})(d+p_{1}-q_{2})}{(b-p_{2}+q_{1})(d-p_{1}+q_{2})}}.

^[3]^{:p. 77}

தொடுநாற்கரம் மற்றொரு வகை நாற்கரமாக இருப்பதற்கான கட்டுப்பாடுகள்[தொகு]

சாய்சதுரம்[தொகு]

ஒரு தொடுநாற்கரத்தின் எதிர்கோணங்கள் சமமாக இருந்தால், இருந்தால் மட்டுமே, அது ஒரு சாய்சதுரமாகும்.^[29]

பட்டம்[தொகு]

பின்வரும் முடிவுகளுள் ஏதாவது ஒன்று உண்மையாக இருந்தால், இருந்தால் மட்டுமே, ஒரு தொடுநாற்கரம் பட்டமாக இருக்க முடியும்:^[15]

மூலைவிட்ட நீளங்களின் பெருக்குத்தொகையில் பாதியாக நாற்கரப் பரப்பளவு இருக்க வேண்டும்.
மூலைவிட்டங்கள் ஒன்றுக்கொன்று செங்குத்தாக இருக்க வேண்டும்.
எதிரெதிர் தொடுநிலைப் புள்ளிகளை இணைக்கும் கோட்டுத்துண்டுகள் (தொடுநிலை நாண்கள்) சமநீளமுள்ளவை
ஒரு சோடி எதிர் தொடுகோட்டு நீளங்கள் சமம்
தொடுநாற்கரத்தின் இருநடுக்கோடுகள் சமநீளமுள்ளவை.
தொடுநாற்கரத்தின் எதிர்பக்க நீளங்களின் பெருக்குத்தொகைகள் சமம்.
சுழற்சி அச்சாகவுள்ள மூலைவிட்டத்தின் மீது உள்வட்டமையம் அமையும்.

இருமைய நாற்கரம்[தொகு]

நாற்கரம் ABCD இன் பக்கங்களை (AB, BC, CD, DA) உள்வட்டம் தொடும் புள்ளிகள் முறையே, W, X, Y, Z எனில், கீழுள்ள முடிவுகளில் ஏதாவது ஒன்று உண்மையாக இருந்தால், இருந்தால் மட்டுமே, நாற்கரம் இருமைய நாற்கரமாக இருக்கும்:^[30]^[1]^:p.124^[18]

WY, XZ க்கு செங்குத்து.
$AW\cdot CY=BW\cdot DY$
${\frac {AC}{BD}}={\frac {AW+CY}{BX+DZ}}$

முதல் முடிவிலிருந்து நாற்கரம் WXYZ, ஒரு செங்குத்து மூலைவிட்ட நாற்கரம் என அறியலாம்.

சமமான தொடர் பக்க நீளங்களுடைய தொடுநாற்கரங்களில், மிக அதிக உள்வட்ட ஆரமுள்ள நாற்கரமே இரு மைய நாற்கரமாக இருக்கும்.^[31]^{:pp.392–393}

சரிவகம்[தொகு]

தொடுநாற்கரத்தின் AB, CD பக்கங்களை உள்வட்டம் தொடும்புள்ளிகள் முறையே W, Y எனில், கீழுள்ள முடிவு உண்மையாக இருந்தால், இருந்தால் மட்டுமே, தொடுநாற்கரம் ABCD ஆனது AB, CD பக்கங்களை இணைபக்கங்களாகக் கொண்ட சரிவகமாக இருக்கும்:^[32]^{:Thm. 2}

AW\cdot DY=BW\cdot CY

AD, BC இணைபக்கங்களாகக் கொண்ட சரிவகமாக இருப்பதற்கு:

AW\cdot BW=CY\cdot DY.

இவற்றையும் பார்க்கவும்[தொகு]

உசாத்துணை[தொகு]

↑ ^1.0 ^1.1 ^1.2 ^1.3 ^1.4 ^1.5 ^1.6 ^1.7 ^1.8 Josefsson, Martin (2010), "Calculations concerning the tangent lengths and tangency chords of a tangential quadrilateral" (PDF), Forum Geometricorum, 10: 119–130.
↑ ^2.0 ^2.1 ^2.2 ^2.3 ^2.4 Andreescu, Titu; Enescu, Bogdan (2006), Mathematical Olympiad Treasures, Birkhäuser, pp. 64–68.
↑ ^3.0 ^3.1 ^3.2 ^3.3 ^3.4 ^3.5 ^3.6 ^3.7 Josefsson, Martin (2011), "More Characterizations of Tangential Quadrilaterals" (PDF), Forum Geometricorum, 11: 65–82.
↑ ^4.0 ^4.1 ^4.2 Minculete, Nicusor (2009), "Characterizations of a Tangential Quadrilateral" (PDF), Forum Geometricorum, 9: 113–118.
↑ Josefsson, Martin (2012), "Similar Metric Characterizations of Tangential and Extangential Quadrilaterals" (PDF), Forum Geometricorum, 12: 63–77
↑ ^6.0 ^6.1 ^6.2 ^6.3 ^6.4 Durell, C.V.; Robson, A. (2003), Advanced Trigonometry, Dover reprint, pp. 28–30.
↑ ^7.0 ^7.1 ^7.2 Hajja, Mowaffaq (2008), "A condition for a circumscriptible quadrilateral to be cyclic" (PDF), Forum Geometricorum, 8: 103–106.
↑ Siddons, A.W.; Hughes, R.T. (1929), Trigonometry, Cambridge Univ. Press, p. 203.
↑ ^9.0 ^9.1 ^9.2 ^9.3 ^9.4 ^9.5 ^9.6 ^9.7 Grinberg, Darij, Circumscribed quadrilaterals revisited, 2008
↑ ^10.0 ^10.1 Yiu, Paul, Euclidean Geometry, [1], 1998, pp. 156–157.
↑ "Post at Art of Problem Solving, 2012". Archived from the original on 2014-02-20. பார்க்கப்பட்ட நாள் 2022-05-29.
↑ Hoyt, John P. (1984), "Quickies, Q694", Mathematics Magazine, 57 (4): 239, 242.
↑ Josefsson, Martin (2010), "On the inradius of a tangential quadrilateral" (PDF), Forum Geometricorum, 10: 27–34.
↑ Bogomolny, Alexander (2016), An Inradii Relation in Inscriptible Quadrilateral, Cut-the-knot, [2].
↑ ^15.0 ^15.1 ^15.2 Josefsson, Martin (2011), "When is a Tangential Quadrilateral a Kite?" (PDF), Forum Geometricorum, 11: 165–174.
↑ Josefsson, Martin (2011), "The Area of a Bicentric Quadrilateral" (PDF), Forum Geometricorum, 11: 155–164.
↑ Gutierrez, Antonio, "Circumscribed Quadrilateral, Diagonal, Chord, Proportion", [3], Accessed 2012-04-09.
↑ ^18.0 ^18.1 ^18.2 Josefsson, Martin (2010), "Characterizations of Bicentric Quadrilaterals" (PDF), Forum Geometricorum, 10: 165–173.
↑ Myakishev, Alexei (2006), "On Two Remarkable Lines Related to a Quadrilateral" (PDF), Forum Geometricorum, 6: 289–295.
↑ Dergiades, Nikolaos; Christodoulou, Dimitris M. (2017), "The two incenters of an arbitrary convex quadrilateral" (PDF), Forum Geometricorum, 17: 245–254.
↑ Andreescu, Titu; Feng, Zuming (2005), 103 Trigonometry Problems From the Training of the USA IMO Team, Birkhäuser, pp. 176–177.
↑ "Determine ratio OM/ON", Post at Art of Problem Solving, 2011^{[தொடர்பிழந்த இணைப்பு]}
↑ Barton, Helen (1926), "On a circle attached to a collapsible four-bar", American Mathematical Monthly, 33 (9): 462–465, doi:10.2307/2299611, JSTOR 2299611.
↑ Bogomolny, Alexander, "When A Quadrilateral Is Inscriptible?", Interactive Mathematics Miscellany and Puzzles, [4].
↑ Chao, Wu Wei; Simeonov, Plamen (2000), "When quadrilaterals have inscribed circles (solution to problem 10698)", American Mathematical Monthly, 107 (7): 657–658, doi:10.2307/2589133.
↑ ^26.0 ^26.1 Vaynshtejn, I.; Vasilyev, N.; Senderov, V. (1995), "(Solution to problem) M1495", Kvant (6): 27–28.
↑ Josefsson, Martin (2012), "Characterizations of Orthodiagonal Quadrilaterals" (PDF), Forum Geometricorum, 12: 13–25.
↑ Hoehn, Larry (2011), "A new formula concerning the diagonals and sides of a quadrilateral" (PDF), Forum Geometricorum, 11: 211–212.
↑ De Villiers, Michael (2011), "Equiangular cyclic and equilateral circumscribed polygons", Mathematical Gazette, 95 (March): 102–107.
↑ Bryant, Victor; Duncan, John (2010), "Wheels within wheels", The Mathematical Gazette, 94 (November): 502–505.
↑ Hess, Albrecht (2014), "On a circle containing the incenters of tangential quadrilaterals" (PDF), Forum Geometricorum, 14: 389–396.
↑ Josefsson, Martin (2014), "The diagonal point triangle revisited" (PDF), Forum Geometricorum, 14: 381–385.

வெளி இணைப்புகள்[தொகு]

Weisstein, Eric W., "Tangential Quadrilateral", MathWorld.

[Josefsson-1] 1.0 ^1.1 ^1.2 ^1.3 ^1.4 ^1.5 ^1.6 ^1.7 ^1.8 Josefsson, Martin (2010), "Calculations concerning the tangent lengths and tangency chords of a tangential quadrilateral" (PDF), Forum Geometricorum, 10: 119–130.

[Andreescu-2] 2.0 ^2.1 ^2.2 ^2.3 ^2.4 Andreescu, Titu; Enescu, Bogdan (2006), Mathematical Olympiad Treasures, Birkhäuser, pp. 64–68.

[Josefsson2-3] 3.0 ^3.1 ^3.2 ^3.3 ^3.4 ^3.5 ^3.6 ^3.7 Josefsson, Martin (2011), "More Characterizations of Tangential Quadrilaterals" (PDF), Forum Geometricorum, 11: 65–82.

[Minculete-4] 4.0 ^4.1 ^4.2 Minculete, Nicusor (2009), "Characterizations of a Tangential Quadrilateral" (PDF), Forum Geometricorum, 9: 113–118.

[5] Josefsson, Martin (2012), "Similar Metric Characterizations of Tangential and Extangential Quadrilaterals" (PDF), Forum Geometricorum, 12: 63–77

[Durell-6] 6.0 ^6.1 ^6.2 ^6.3 ^6.4 Durell, C.V.; Robson, A. (2003), Advanced Trigonometry, Dover reprint, pp. 28–30.

[Hajja-7] 7.0 ^7.1 ^7.2 Hajja, Mowaffaq (2008), "A condition for a circumscriptible quadrilateral to be cyclic" (PDF), Forum Geometricorum, 8: 103–106.

[8] Siddons, A.W.; Hughes, R.T. (1929), Trigonometry, Cambridge Univ. Press, p. 203.

[Grinberg-9] 9.0 ^9.1 ^9.2 ^9.3 ^9.4 ^9.5 ^9.6 ^9.7 Grinberg, Darij, Circumscribed quadrilaterals revisited, 2008

[Yiu-10] 10.0 ^10.1 Yiu, Paul, Euclidean Geometry, [1], 1998, pp. 156–157.

[11] "Post at Art of Problem Solving, 2012". Archived from the original on 2014-02-20. பார்க்கப்பட்ட நாள் 2022-05-29.

[12] Hoyt, John P. (1984), "Quickies, Q694", Mathematics Magazine, 57 (4): 239, 242.

[13] Josefsson, Martin (2010), "On the inradius of a tangential quadrilateral" (PDF), Forum Geometricorum, 10: 27–34.

[14] Bogomolny, Alexander (2016), An Inradii Relation in Inscriptible Quadrilateral, Cut-the-knot, [2].

[Josefsson3-15] 15.0 ^15.1 ^15.2 Josefsson, Martin (2011), "When is a Tangential Quadrilateral a Kite?" (PDF), Forum Geometricorum, 11: 165–174.

[16] Josefsson, Martin (2011), "The Area of a Bicentric Quadrilateral" (PDF), Forum Geometricorum, 11: 155–164.

[17] Gutierrez, Antonio, "Circumscribed Quadrilateral, Diagonal, Chord, Proportion", [3], Accessed 2012-04-09.

[Josefsson4-18] 18.0 ^18.1 ^18.2 Josefsson, Martin (2010), "Characterizations of Bicentric Quadrilaterals" (PDF), Forum Geometricorum, 10: 165–173.

[Myakishev-19] Myakishev, Alexei (2006), "On Two Remarkable Lines Related to a Quadrilateral" (PDF), Forum Geometricorum, 6: 289–295.

[20] Dergiades, Nikolaos; Christodoulou, Dimitris M. (2017), "The two incenters of an arbitrary convex quadrilateral" (PDF), Forum Geometricorum, 17: 245–254.

[21] Andreescu, Titu; Feng, Zuming (2005), 103 Trigonometry Problems From the Training of the USA IMO Team, Birkhäuser, pp. 176–177.

[22] "Determine ratio OM/ON", Post at Art of Problem Solving, 2011^{[தொடர்பிழந்த இணைப்பு]}

[23] Barton, Helen (1926), "On a circle attached to a collapsible four-bar", American Mathematical Monthly, 33 (9): 462–465, doi:10.2307/2299611, JSTOR 2299611.

[24] Bogomolny, Alexander, "When A Quadrilateral Is Inscriptible?", Interactive Mathematics Miscellany and Puzzles, [4].

[25] Chao, Wu Wei; Simeonov, Plamen (2000), "When quadrilaterals have inscribed circles (solution to problem 10698)", American Mathematical Monthly, 107 (7): 657–658, doi:10.2307/2589133.

[Vaynshtejn-26] 26.0 ^26.1 Vaynshtejn, I.; Vasilyev, N.; Senderov, V. (1995), "(Solution to problem) M1495", Kvant (6): 27–28.

[27] Josefsson, Martin (2012), "Characterizations of Orthodiagonal Quadrilaterals" (PDF), Forum Geometricorum, 12: 13–25.

[28] Hoehn, Larry (2011), "A new formula concerning the diagonals and sides of a quadrilateral" (PDF), Forum Geometricorum, 11: 211–212.

[29] De Villiers, Michael (2011), "Equiangular cyclic and equilateral circumscribed polygons", Mathematical Gazette, 95 (March): 102–107.

[Bryant-30] Bryant, Victor; Duncan, John (2010), "Wheels within wheels", The Mathematical Gazette, 94 (November): 502–505.

[Hess-31] Hess, Albrecht (2014), "On a circle containing the incenters of tangential quadrilaterals" (PDF), Forum Geometricorum, 14: 389–396.

[J2-32] Josefsson, Martin (2014), "The diagonal point triangle revisited" (PDF), Forum Geometricorum, 14: 381–385.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]