ஓமின் விதி

| மின்காந்தவியல் |
|---|
 |
ஒரு [மின்கடத்தி]யில் மின்னழுத்ததைக் கொடுக்கும் போது, அதில் மின்னோட்டம் நடை பெறுகின்றது. அந்த மின்னோட்டத்தின் அளவு அதில் கொடுக்கப்படும் மின்னழுத்தத்தின் அளவைப் பொறுத்திருக்கும். எடுத்துக் காட்டாக, R என்ற மின்தடையம் கொண்ட ஒரு மின் கடத்தியின்(எ.கா. உலோகங்கள்,மாழைகள்) இரு முனைகளுக்கிடையே, V என்ற அளவு மின்னழுத்தம்(voltage) கொடுக்கும் போது, I என்ற அளவு மின்னோட்டம்(current) பாய்கிறது என்றால், அந்த மின்னோட்டத்தின் அளவைக் கீழ்க் கண்டவாறு கணக்கிடலாம்:
- .
இந்தக் கருத்தை ஜார்ஜ் ஓம் (Georg Ohm) என்ற செருமானிய அறிஞர் 1827-இல் முன் வைத்தார்.அவர் கூறிய இக் கருத்து ஓமின் விதி என்று பின்னால் வழங்கப் பட்டது.[1] சுருங்கக் கூறின், ஒரு மின்கடத்தியில் ஓடும் மின்னோட்டம் I அதன் இரு முனைகட்கு நடுவில் கொடுக்கப்படும் மின்னழுத்தம் V-இன் மீது நேர் விகிதச் சார்பு கொண்டிருக்கும் என்பதுதான் ஓமின் விதி. அதாவது,
வேறுவிதமாகக் கூறுவதென்றால், மின்னழுத்தத்திற்கும், மின்னோட்டத்திற்கும் இடையேயான விகிதம் ஒரு மாறிலி ஆகும். அதாவது,
இந்த மாறிலி எண் R என்பதே மின் தடை எனப்படும்.[2]
மின்தடையின் அலகு ஓம் (Ω) (Ohm) ஆகும். ஓம் என்ற அலகு,வோல்ட்டு/ஆம்ப்பியர் (volt/ampere),(வோல்ட்டு-நொடி/கூலாம்) (volt-second/coulomb) ஆகிய அலகுகளுக்கு இணையானது.

ஓமின் விதியை, இயற்பியல் துறையில் சற்று மாற்றி எழுதுவார்கள். ஒரு மின்கடத்தியின் வழியாகப் பாயும் மின்சாரத்தின் மின்னோட்டச் செறிவு ஒரு புள்ளியில் J எனவும், அதே புள்ளியில் மின்புலம் E எனவும், அந்த மின்கடத்தியின் மின்கடத்துதிறன் மற்றும் மின்தடைத்திறன் எனவும் வைத்துக் கொண்டால், ஓமின் விதியை
என்றும் எழுதலாம்.[3]
வரலாறு[தொகு]

ஜார்ஜ் ஓம் அவர்களுக்கு முன்னரே, 1781-இல், என்றி காவன்டிஷ்(Henry Cavendish) என்பவர், வேவ்வேறு அளவுள்ள கண்ணாடிக் குழாய்களில் உப்பு நீரை அடைத்து, அவற்றுள் மினசாரத்தைச் செலுத்தி, பல ஆய்வுகளைச் செய்தார். அதன் படி, மின்னழுத்த அளவு மாறினால் மின்னோட்டம் அளவும் மாறும் என்று கண்டறிந்தார். ஆனால், தம் கண்டுபிடிப்பை மற்ற ஆய்வாளர்கள் யாரிடமும் சொல்லாமல் விட்டு விடவே, இதைப் பற்றி யாருக்கும் தெரியாமல் போய் விட்டது.[4] அதற்குப் பிறகு வந்த ஜேம்சு கிளார்க் மாக்சுவெல்(James Clerk Maxwell) என்ற அறிவியல் அறிஞர் அந்தக் கண்டுபிடிப்பை 1879-இல் வெளியிட்டார்.[5]
ஓம் தம்முடைய ஆராய்ச்சியை 1825–1826 ஆண்டுகளில் செய்து, தம் கண்டு பிடிப்புகளை 1827-இல் Die galvanische Kette, mathematisch bearbeitet ("மின் சுற்று - ஓர் கணித முறை ஆய்வு")என்ற நூலாக வெளியிட்டார்.[6] தன்னுடைய ஆய்வில் அவர் கண்டறிந்ததைக் கீழ்க்கண்ட சமன்பாடாக எழுதினர்:
இதில், மின்னோட்டத்தின் அளவையும், மின் கடத்தியின் நீளத்தையும், அவர் மின்கலனாகப் பயன்படுத்திய வெப்பமின் இரட்டையின் வெப்பநிலையையும் குறிக்கும். மற்றும், என்பது அவர் செய்த சோதனையைச் சார்ந்த ஒரு மாறிலி(constant) எண் ஆகும்.
இந்தக் கண்டு பிடிப்பை மற்ற ஆய்வாளர்கள் முதலில் ஏற்றுக் கொள்ளவில்லை.[7][8] 1840-உக்குப் பிறகே, அவர் கண்டுபிடிப்பை மற்றவர்கள் ஏற்றுக்கொண்டு, அவருக்கு உரிய மதிப்பைக் கொடுத்தனர்.
ஓமின் விதி எல்லா இடங்களிலும் சரியான விடை தருமா?[தொகு]
ஓமின் விதி எல்லா இடங்களிலும் சரியான விடையைத் தருமா என்று தெரியாமல் இருந்தது. ஓமின் விதியில் ஒரு சில குறைகள் இருப்பதாக சிலர் நினைத்தனர். 1920-இல், மின்கடத்தி வழியாகச் செல்லும் மின்னோட்டம் மின்கடத்தியின் எல்லா இடங்களிலும் ஒரே அளவாக இருப்பதில்லை எனக் கண்டு பிடிக்கப்பட்டது. ஒவ்வொரு இடத்திலும் மின்னோட்டம் மாறி இருப்பதற்குக் காரணம் ஜான்சன்-நைகிஸ்ட் இரைச்சல் எனப்படும் ஒரு வகை மின்னிரைச்சல் என்று கருதப் பட்டது. அதனால், ஒரு மின்கடத்தியில், மின்தடையின் மதிப்பு எல்லா இடங்களிலும் ஒரே அளவாக இருப்பதில்லை என்றும் கருதப் பட்டது.
எனவே, ஓமின் விதியை எல்லா இடங்களிலும் அப்படியே பயன்படுத்த இயலாது என்று தெரிய வந்தது. எடுத்துக் காட்டாக, ஒரு மின்கடத்தியின் இரு முனைகளிலும் மிக அதிக அளவில் மின்னழுத்தம் கொடுக்கும் போது, மின்கடத்திக்குள் மிக வன்மையான மின்புலம் உருவாகின்றது. இதனால், மின்கடத்தியில் மின் முறிவு ஏற்பட வழியுண்டு. அவ்வாறு மின் முறிவு ஏற்பட்டால், ஓமின் விதியின் படி எதிர் பார்த்ததைவிட மிக அதிக அளவிலான மின்சாரம் பாயும். அது போலவே, ஒரு சில மின் கடத்திகளில், மிகக் குறைவான மின் அழுத்தம் கொடுக்கும் போது, ஓமின் விதியின் படி எதிர்பார்த்த அளவு மின்னோட்டம் ஓடுவதில்லை.[9] [10]
இருப்பினும், ஓமின் விதி பல இடங்களில் சரியாகவே இருக்கின்றது. அணு அளவில் நடக்கும் மின்னோட்டம் ஓமின் விதி சொல்வது போல் இருக்காது என்று 20-ஆம் நூற்றாண்டில் எதிர் பார்க்கப் பட்டது. ஆனால், அது தொடர்பான நடத்திய ஆய்வுகளில், அணு அளவிலும் ஓமின் விதி சரியாகவே செயல் படுகின்றது என்று ஏற்றுக் கொள்ளப் பட்டது. சொல்லப் போனால், 2012-இல் நடத்தப் பட்ட ஆய்வுகளின் படி, நான்கு அணுக்கள் அகலமும், ஒரு அணு உயரமும் கொண்ட சிலிகான் கம்பிகளில் கூட ஓமின் விதி சரியாகவே செயல் படுகின்றது என்று அறியப் பட்டது.[11]
அணு அளவிலான விளக்கங்கள்[தொகு]

ஓமின் விதியை அணு அளவில் எவ்வாறு புரிந்து கொள்வது(microscopic origin of Ohm's law) என்பது பற்றி செருமானிய அறிவியலாளர் பால் ட்ரூட்(Paul Drude) 1900-இல் ஒரு விளக்கம் கொடுத்தார்.[12][13] இதன் படி, ஒரு மின் கடத்தியில் மின்னழுத்ததைக் கொடுக்கும் போது அதில் மின்புலம் உருவாகின்றது. அந்த மின்புலம் மின்கடத்தியில் உள்ள எதிர்மின்னிகளைக் கவர்ந்து இழுத்து ஒரே திசையில் ஓட வைக்கின்றது. எதிர்மின்னிகள் ஓடும் போது மின்கடத்தியில் உள்ள அணுக்கள் மீது மோதி சிதறி திசை மாறுகின்றன. திசை மாறிய எதிர்மின்னிகள் மற்ற அணுக்களோடு மீண்டும் மோதிச் சிதறுகின்றன. இருப்பினும், மொத்தத்தில், ஒரு திசையை நோக்கி எதிர்மின்னிகள் கொஞ்சம் நகருகின்றன. இவ்வாறு எதிர்மின்னிகள் நகருவதால் மின்கடத்தியில் மின்னோட்டம் நடை பெறுகின்றது. நகருகின்ற எதிர்மின்னிகளின் உந்தம் p, மின்புலத்தின் அளவு E, ஒரு எதிர்மின்னியின் மின்னூட்டம்(charge) -e, மோதல்களுக்கிடையுள்ள நேரம் τ எனக் கொண்டால், p = −eEτ என்று பால் ட்ரூட் கணக்கிட்டுக் கூறினார். இந்தச் சமன்பாட்டின் படி, E அதிகமாகும் போது, p அதிகமாகின்றது; p அதிகமானால், மின்னன்களின் விரைவும் அதிகமாகிறது. அதாவது, மின்னோட்டம் அதிகமாகிறது. ஓமின் விதி சொல்வதும் இதுவே: மின்னழுத்தம் அதிகமாகும் போது மின்னோட்டம் அதிகமாகும்.
மின்னோட்டமும் நீரோட்டமும்[தொகு]
மின்னோட்டத்தை நீரோட்டத்தோடு ஒப்பிட்டும், ஓமின் விதியை விளங்கிக் கொள்ளலாம். நீர் அழுத்தம் என்பது மின்னழுத்தம், நீரோட்டம் என்பது மின்னோட்டம், நீரோட்டத் தடை என்பது மின்தடை என்று கொண்டால், நீர் அழுத்தம் அதிகமானால் நீரோட்டமும் அதிகமாகும் என்பது மின்னழுத்தம் அதிகமாகும் போது மின்னோட்டம் அதிகமாகும் என்ற ஓமின் விதி போன்று உள்ளது எனலாம்.(நீரோட்டத் தடை என்பது நீரோட்டத்தைக் குறைப்பதற்காக வைக்கப் படும் தடைகள் ஆகும்.)
மின்சுற்று பகுப்பாய்வு[தொகு]
ஓமின் விதி மின் சுற்றுகளைப் பகுத்து அலசிப் பார்க்க பெரிதும் துணையாக இருக்கும். ஓமின் சமன்பாட்டைக் கீழ்க் கண்டவாறு நாம் எப்படி வேண்டுமானாலும் எழுதிக் கொள்ளலாம்: [14][15]
இந்தச் சமன் பாடுகள் மின் சுற்றுகளில் ஓடும் மின்னோட்டம், தோன்றும் மின்னழுத்தம், அடங்கியுள்ள மின் தடை ஆகியனவற்றைக் கணக்கிட பெரிதும் உதவியாக இருக்கும்.
சுற்றுகள்[தொகு]
மின்தடைச் சுற்றுகள் என்பது மின்தடைகள் மட்டுமே கொண்ட மின் சுற்றுகள் ஆகும். இதில் மின்தேக்கி, மின்தூண்டி போன்ற மின் உறுப்புகள் (மின்கூறுகள்)இருக்காது. இப்படிப் பட்ட சுற்றுக்களை ஓமின் விதி கொண்டு ஒவ்வொரு புள்ளியிலும் எவ்வளவு மின் அழுத்தம் உள்ளது, ஒவ்வொரு மின் தடையிலும் எவ்வளவு மின்னோட்டம் செல்கிறது என்று எளிதாகக் கணக்கிட முடியும்.
எதிர்இயக்கச் சுற்றுக்கள்[தொகு]
எதிர்இயக்கச் சுற்று என்பது மின் தடை R, எதிர் இயக்கப் பொருள்களான மின்தேக்கி C , மின்தூண்டி L ஆகிய மின் கூறுகள் கலந்த மின் சுற்று ஆகும். இது போன்ற சுற்றுக்களில், நேர் மின்னோட்டத்தைக் காட்டிலும், மாறுதிசை மின்னோட்டமே பெரிதும் செலுத்தப் படும். மாறுதிசை மின்னோட்டத்தின் அதிர்வெண் என்று வைத்துக் கொண்டால், -இன் மின்னெதிர்ப்பு எனவும், -இன் மின்னெதிர்ப்பு எனவும் இருக்கும். இதில், , மற்றும் கற்பனை எண் . மின்னியலில், என்பதை என்ற எழுத்தாலும், மின்னெதிர்ப்பை என்ற எழுத்தாலும் குறிப்பிடுவர். எனவே, ஓமின் விதியைக் கீழ்க் கண்டவாறும் குறிப்பிடலாம்:[16]
மின்தூண்டி L-இன் மின்னெதிர்ப்பு:
மின்தேக்கி C -இன் மின்னெதிர்ப்பு:
ஓமின் விதி:
நேர்ச்சார்பு உள்ளமை[தொகு]
எல்லா மின் பொருட்களும் ஓமின் விதிப்படிச் செயல் படுவதில்லை. எடுத்துக்கட்டாக, இருமுனையம், மின்கலம் ஆகிய மின்கூறுகள் ஓமின் விதியைப் பின்பற்றுவதில்லை.மின்னோட்டத்துக்கும் மின்னழுத்துக்கும் உள்ள சார்பின் வரைபடம் (0,0) என்ற புள்ளியின் வழியாகச் செல்லும் நேர்க் கோடாக இருக்க வேண்டும். நேர்க் கோட்டின் சாய்வின் அளவு மின்கடத்துதிறனைக் குறிக்கும்.

படத்தில், மின்தடையத்தின் I–V வரைபடம் நேர்க்கோடாக இருக்கிறது. எனவே, மின்னோட்டம் I, மின்னழுத்தம் V -உடன் நேர் விகிதச் சார்பு கொண்டதாக உள்ளது. ஆனால், இருமுனையத்தின் I–V வரைபடம் நேர்க் கோடாக இல்லை.(படத்தைப் பார்க்க.) ஒவ்வொரு புள்ளியிலும் சாய்வின் அளவு மாறிக் கொண்டே போகின்றது. மேலும், மின்கலத்தின் I-V வரைபடம், நேர்க் கோடாக இருப்பினும், (0,0) என்ற புள்ளி வழியாகச் செல்லவில்லை. இது போன்ற பொருட்களில் மின்னோட்டத்தைக் கணக்கிட ஓமின் விதி பயன்படாது.
மின்கடத்தியின் மீது வெப்பத்தின் விளைவுகள்[தொகு]
ஓமின் விதிப்படி, மின்கடத்தியில் வேறு எந்த மாற்றமும் நிகழாத போதுதான், மின்னழுத்தம் அதிகரிக்க மின்னோட்டமும் அதிகரிக்கும். ஆனால், ஒரு மின்கடத்தியின் வழியாக மின்சாரம் பாயும் போது, ஜூல் விளைவின் படி, அக் கடத்தி சூடாகிறது. சூடு அதிகமாகும் போது, கடத்தியின் மின்தடை அதிகரிக்கின்றது.[17] எனவே, மின்னோட்டம் நடக்கும் போது மின்தடை மாறுவதால், ஓமின் விதியை இங்கு நாம் பயன்படுத்த முடியாமல் போய் விடுகிறது. மாக்ஸ்வெல் என்ற ஸ்காட்லாந்தைச் சேர்ந்த இயல்பியல் அறிஞர், மின்கடத்தியில் உண்டாகும் வெப்பத்தைக் குறைத்து ஓமின் விதியை எப்படி நிறுவுவது என்று பல ஆய்வுகள் நடத்தி 1876-இல் தம் ஆய்வு முடிவுகளை வெளியிட்டுள்ளார்.[18]
வெப்ப ஓட்டமும் ஓமின் விதியும்[தொகு]
ஒரு மின்கடத்தியில், இரு புள்ளிகளுக்கிடையில் மின்னழுத்த வேறுபாடு இருக்கும் போது அக் கடத்தியில் மின்னோட்டம் நடப்பது போல, ஒரு வெப்பக்கடத்தியில், பிரெஞ்சுக் கணிதவியலாளரான பூரியே அவர்களின் கூற்றுப்படி, இரு புள்ளிகளுக்கிடையே வெப்ப வேறுபாடு இருக்கும் போது, அதில் வெப்ப ஓட்டம் நடை பெறும். அவ்வாறு நடக்கின்ற வெப்ப ஓட்டம், ஓமின் விதி போலவே, புள்ளிகளுக்கிடையே உள்ள வெப்ப வேறுபாட்டின் அளவைப் பொறுத்து இருக்கும்.
ஓமின் விதியின் ஏனைய வடிவங்கள்[தொகு]
இயல்பியலில் V = IR என்ற ஓமின் விதியை,
என்று எழுதுவார்கள்[19]. இதில், E என்பது மின்புலத்தின் வலிமை, ρ என்பது மின்தடைத் திறன், மற்றும் J என்பது மின்னோட்டச் செறிவும் ஆகும். (கவனிக்க: , உங்கே என்பது மின் கடத்தியின் பரப்பளவு, என்பது மின் கடத்தியின் நீளம் ஆகும்.)
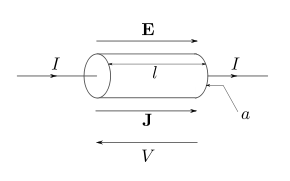
ஒரு மின்கடத்தியில் E என்ற மின்புலம் இருந்தால், அதில் இரு புள்ளிகளுக்கிடையே உள்ள மின்னழுத்தை கீழ்க் கண்டவாறு கணக்கிலாம்:[20]
இதில், dl என்பது கடத்தியின் நீளத்தில் மிகச் சிறு (நுண்ணிய) அளவைக் குறிக்கும். மின்புலம் E மின்கடத்தியில் எந்த இடத்திலும் மாறாது ஒரே மதிப்பு உள்ளதாக இருந்தால், மின்கடத்தியின் நீளம் l எனவும் கொண்டால், மேற்கண்ட சமன்பாட்டை கீழ்க் கண்டவாறு எழுதலாம்:
இனி, கடத்தியின் மின்தடைத்திறனும் ஒரு சீராக இருந்தால், மின்னோட்டச் செறிவும் கடத்தி முழுவதும் ஒரு சீராக இருக்கும் எனலாம். எனவே,a என்ற குறுக்கு வெட்டுப் பரப்பளவு கொண்ட மின் கடத்தியில், மின்னோட்டச் செறிவைக் கீழ்க் கண்டவாறு எழுதலாம்:
மேற்கண்ட சமன்பாடுகளில் இருந்து, மின்னழுத்தம் V-ஐக் கணிக்கலாம்:
மின்தடைத்திறன் ρ எனவும், l என்ற நீளமும், a என்ற குறுக்கு வெட்டுப் பரபளவும் உள்ள ஒரு மின்கடத்தியின் மின்தடையத்தை கீழ்க் கண்டவாறு எழுலாம்:[21]
மேற்கண்ட சமன்பாடுகளில் இருந்து, ஓமின் விதியைத் தருவிக்கலாம்:
காந்தப் புலத்தின் தாக்கம்[தொகு]
ஓமின் விதி, E அளவுள்ள மின்புலத்தினால் R அளவு மின்தடை கொண்ட ஒரு மின்கடத்தியில் எவ்வளவு மின்னோட்டம் ஓடுகின்றது என்று சொல்கின்றது. ஒரு மின்கடத்தி B என்ற அளவுள்ள ஒரு காந்தப் புலத்தில் v என்ற வேகத்தோடு நகரும் பொது, v x B என்ற அளவுக்கு மின்புலம் உருவாக்கப் படுகின்றது. இதனால், மின்கடத்தியில் உள்ள மொத்த மின்புலம் E + v x B என்றாகிறது. அதனால், மின்கடத்தியில் கூடுதல் மின்னோட்டம் நடைபெறுகின்றது:
மின்கடத்திப் பாய்மங்கள்[தொகு]
மின்சாரத்தைக் கடத்தும் தன்மை கொண்ட பாய்மங்களை மின்கடத்திப் பாய்மங்கள் எனச் சொல்லலாம். மின்மக் கலவை(பிளாசுமா) போன்றவை இதற்கு எடுத்துக் காட்டுகளாகும். மின்கடத்தி ஒன்றில் செல்லும் எதிர்மின்னிகளை ஒரு புகை மண்டலமாக நினைத்துக் கொள்ளலாம். இது என்ற வேகத்தோடு என்ற அளவு கொண்ட காந்தப் புலத்தில் நகர்கின்றது என்றும், மின்கடத்தியில் உள்ள அணுக்கள் வேகம் என்றும் கொண்டால், மின் கடத்தியில் என்ற அளவுள்ள மின் புலம் உருவாகும். இந்த மின்புலம் என்ற அளவு கொண்ட மின்னொட்டச் செறிவை உருவாக்கும். இந் நிலையில், எதிர் மின்னிப் பாய்மத்தின் இயக்கச் சமன்பாட்டைக் கீழ்க் கண்டவாறு எழுதலாம்:
இதில், என்பது எதிர் மின்னிகளின் அடர்த்தி; , and என்பவை, முறையே எதிர்மின்னியின் மின்ம அளவு, திணிவு, வேகம் என்பனவற்றைக் குறிக்கும். மற்றும், என்பது ஒரு எதிர் மின்னி அணுக்களோடு ஒரு வினாடிக்கு எத்தனை முறை மோதுகிறது என்பதையும் குறிக்கும். மேலும், என்பது அணுக்களின் வேகத்தைக் குறிக்கின்றது. இனி, எதிர் மின்னியின் திணிவு அணுக்களின் திணிவைக் காட்டிலும் மிக மிகக் குறைந்ததாக இருப்பதால், மேற் கண்ட சமன்பாட்டில், இடது புறத்தில் உள்ள கோவையை 0 என்று வைத்துக் கொண்டு, சமன்பாட்டை இவ்வாறு சுருக்கி எழுதலாம்:
இதில், J என்பது மின்னோட்டச் செறிவாகும். மேலும், என்பது கடத்தியின் மின்கடத்துத்திறனைக் குறிக்கின்றது. மேலுள்ள சமன்பாட்டை
என்றும் எழுதலாம். இதில் மின்தடைத்திறனைக் குறிக்கும்.
உசாத்துணை[தொகு]
- ↑ Robert A. Millikan and E. S. Bishop (1917). Elements of Electricity. American Technical Society. p. 54.
- ↑ Oliver Heaviside (1894). Electrical papers 1. Macmillan and Co. p. 283. ISBN 0-8218-2840-1.
- ↑ Olivier Darrigol, Electrodynamics from Ampère to Einstein, p.70, Oxford University Press, 2000 ISBN 0-19-850594-9.
- ↑ "Electricity". Encyclopædia Britannica. 1911.
- ↑ Sanford P. Bordeau (1982) Volts to Hertz...the Rise of Electricity. Burgess Publishing Company, Minneapolis, MN. pp.86–107, ISBN 0-8087-4908-0
- ↑ G. S. Ohm (1827). Die galvanische Kette, mathematisch bearbeitet. Berlin: T. H. Riemann. http://www.ohm-hochschule.de/bib/textarchiv/Ohm.Die_galvanische_Kette.pdf.
- ↑ Davies, B, "A web of naked fancies?", Physics Education 15 57–61, Institute of Physics, Issue 1, Jan 1980 [1]
- ↑ Hart, IB, Makers of Science, London, Oxford University Press, 1923. p. 243. [2] பரணிடப்பட்டது 2008-03-08 at the வந்தவழி இயந்திரம்
- ↑ Purcell, Edward M. (1985), Electricity and magnetism, Berkeley Physics Course, vol. 2 (2nd ed.), McGraw-Hill, p. 129, ISBN 0-07-004908-4
- ↑ Griffiths, David J. (1999), Introduction to electrodynamics (3rd ed.), Prentice Hall, p. 289, ISBN 0-13-805326-X
- ↑ Weber, B.; Mahapatra, S.; Ryu, H.; Lee, S.; Fuhrer, A.; Reusch, T. C. G.; Thompson, D. L.; Lee, W. C. T. et al. (2012). "Ohm's Law Survives to the Atomic Scale". Science 335 (6064): 64–67. doi:10.1126/science.1214319. http://www.sciencemag.org/content/335/6064/64.
- ↑ Drude, Paul (1900). "Zur Elektronentheorie der metalle". Annalen der Physik 306 (3): 566. doi:10.1002/andp.19003060312. Bibcode: 1900AnP...306..566D. http://www3.interscience.wiley.com/cgi-bin/fulltext/112485959/PDFSTART.[தொடர்பிழந்த இணைப்பு]
- ↑ Drude, Paul (1900). "Zur Elektronentheorie der Metalle; II. Teil. Galvanomagnetische und thermomagnetische Effecte". Annalen der Physik 308 (11): 369. doi:10.1002/andp.19003081102. Bibcode: 1900AnP...308..369D. http://www3.interscience.wiley.com/cgi-bin/fulltext/112485893/PDFSTART.[தொடர்பிழந்த இணைப்பு]
- ↑ James William Nilsson and Susan A. Riedel (2008). Electric circuits. Prentice Hall. பக். 29. பன்னாட்டுத் தரப்புத்தக எண்:978-0-13-198925-2. http://books.google.com/?id=sxmM8RFL99wC&pg=PA29&dq=%22Ohm%27s+law+expresses+the+voltage%22++%22V+%3D+iR%22.
- ↑ Alvin M. Halpern and Erich Erlbach (1998). Schaum's outline of theory and problems of beginning physics II. McGraw-Hill Professional. பக். 140. பன்னாட்டுத் தரப்புத்தக எண்:978-0-07-025707-8. http://books.google.com/?id=vN2chIay624C&pg=PA140&dq=%22Ohm%27s+law+that+R%3D+V/I+is+a+constant%22.
- ↑ Rajendra Prasad (2006). Fundamentals of Electrical Engineering. Prentice-Hall of India. ISBN 978-81-203-2729-0.
- ↑ en:Electrical resistance and conductance
- ↑ Normal Lockyer, தொகுப்பாசிரியர் (September 21, 1876). "Reports". Nature (Macmillan Journals Ltd) 14: 451–9 [452]. doi:10.1038/014451a0. Bibcode: 1876Natur..14..451.. http://books.google.com/?id=-8gKAAAAYAAJ&pg=PA452&dq=ohm%27s-law+temperature&q=ohm's-law%20temperature.
- ↑ Lerner, Lawrence S. (1977). Physics for scientists and engineers. Jones & Bartlett. பக். 736. பன்னாட்டுத் தரப்புத்தக எண்:978-0-7637-0460-5. http://books.google.com/?id=Nv5GAyAdijoC&pg=PA736.
- ↑ Lerner L, Physics for scientists and engineers, Jones & Bartlett, 1997, pp. 685–686
- ↑ en:Ohm's law#cite note-lerner732-35
வெளி இணைப்புகள்[தொகு]
- Ohm's Law chapter from Lessons In Electric Circuits Vol 1 DC book and series.
- John C. Shedd and Mayo D. Hershey,"The History of Ohm's Law", Popular Science, December 1913, pages 599-614, Bonnier Corporation
பன்னாட்டுத் தர தொடர் எண் 0161-7370, gives the history of Ohm's investigations, prior work, Ohm's false equation in the first paper, illustration of Ohm's experimental apparatus.
- Morton L. Schagrin, "Resistance to Ohm's Law", American Journal of Physics, July 1963, Volume 31, Issue 7, pp. 536–47. Explores the conceptual change underlying Ohm's experimental work.
- Kenneth L. Caneva, "Ohm, Georg Simon." Complete Dictionary of Scientific Biography. 2008


















































