ஒளிவிலகல் குறிப்பெண்

ஓர் ஊடகத்தின் ஒளிவிலகல் குறிப்பான் (Refractive index) அல்லது ஒளிவிலகலின் குறிப்பான் என்பது ஒரு ஊடகத்திற்குள்ளாக ஒளியின் வேகம் (அல்லது ஒலி அலைகள் போன்ற பிற அலைகள்) எவ்வாறு குறைக்கப்படுகிறது என்பதற்கான அளவீடாகும். உதாரணத்திற்கு, வகைமாதிரியான சோடா-லைம் கண்ணாடியானது 1.5க்கு அருகாமையிலான ஒளிவிலகல் குறிப்பானைக் கொண்டிருக்கிறது, அதாவது இந்தக் கண்ணாடியில் ஒளியானது வெற்றிடத்தில் ஒளியின் வேகமான 1 / 1.5 = 2/3 என்ற அளவில் பயணமாகிறது. கண்ணாடி மற்றும் ஒளி ஊடுருவும் பொருட்களின் இரண்டு பொதுவான உடைமைப்பொருள்கள் அவற்றின் ஒளிவிலகல் குறிப்பானோடு தொடர்புகொண்டிருக்கின்றன. முதலில், ஒளிக் கதிர்கள் காற்றிலிருந்து பொருளுக்கு இடைமுகத்தை கடக்கும்போது திசையை மாற்றிக்கொள்கின்றன, இந்த விளைவு ஆடிகளில் பயன்படுத்தப்படுகிறது. இரண்டாவதாக, ஒளியானது அவற்றைச் சுற்றிலுமிருப்பவற்றிலிருந்து மாறுபடும் ஒளிவிலகல் குறிப்பானைக் கொண்டிருக்கும் மேற்பரப்புகளிலிருந்து பகுதியளவிற்கு பிரதிபலிக்கிறது.

வரையறைகள்

ஒரு ஊடகத்தின் n ஒளிவிலகல் குறிப்பான் அந்த ஊடகத்திற்குள்ளேயான v_p படிநிலை விசைக்கான குறிப்பீட்டு ஊடகத்தில் உள்ள ஒளி அல்லது ஒலி போன்ற அலை நிகழ்வின் c விசையின் விகிதமாக வரையறுக்கப்பட்டிருக்கிறது.

n={\frac {c}{v_{\mathrm {p} }}}.

இது வெற்றிடத்தை குறிப்பீட்டு ஊடகமாகக் கொண்டு ஒளி வகையில் மிகவும் பொதுவாகப் பயன்படுத்தப்படுகிறது, இருப்பினும் வரலாற்றுப்பூர்வமாக மற்ற குறிப்பீட்டு ஊடகமும் (எ.கா. நிலைப்படுத்தப்பட்ட அழுத்தம் மற்றும் வெப்பநிலையில் உள்ள காற்று) பொதுவானதாக இருக்கிறது. இதற்கு வழக்கமாக n என்ற குறியீடு வழங்கப்படுகிறது. ஒளி வகையில் இது பின்வருவதற்கு சமமாக இருக்கிறது,

n={\sqrt {\epsilon _{r}\mu _{r}}},

ε_r பொருள்வய சார்பு பெர்மிட்டிவிட்டியாகவும், μ_r என்பது அதனுடைய சார்பு ஊடுபாவுதலாகவும் இருக்குமிடத்தில். பெரும்பாலான மூலப்பொருள்களுக்கு μ_r என்பது பார்வை நிகழ்வெண்களில் 1க்கு மிக நெருக்கமானதாக இருக்கிறது என்பதால் n ஆனது தோராயமாக ${\sqrt {\epsilon _{r}}}$ என்பதாக இருக்கிறது. பரவலான தவறான கருத்துக்கு மாறாக n ஆனது 1க்கும் குறைவாக இருக்கலாம், உதாரணத்திற்கு எக்ஸ்-கதிர்கள்.^[1] மொத்த வெளிப்புற பிரதிபலிப்பு அடிப்படையிலான எக்ஸ்-கதிர்களுக்கான பயன்மிக்க கண்ணாடிகள் போன்று இது நடைமுறை தொழில்நுட்ப பயன்பாட்டைக் கொண்டதாக இருக்கிறது. பிளாஸ்மாக்களி்ல் உள்ள மின்காந்த அலைகளின் n 1க்கும் குறைவாக இருப்பது மற்றொரு உதாரணம்.

படிநிலை விசையானது அலைவடிவம் பெருக்கமுறுவதன் அலைமுகடு விகிதமாக வரையறுக்கப்படுகிறது; அதாவது அலைவடிவத்தின் படிநிலை நகரும் விகிதம். குழு விசையானது அலைவடிவம் பெருக்கமுறுவதன் மேலுறை விகிதமாக வரையறுக்கப்படுகிறது; அதாவது அலைவடிவத்தின் பெருக்கத்தினுடைய மாறுபாட்டு விகிதம். கொடுக்கப்படும் அலைவடிவம் பெருக்கமுறுதலின்போது குறிப்பிடத்தகுந்த அளவிற்கு சிதறடிக்கச் செய்வதில்லை, இது அலையால் தகவலானது (மற்றும் ஆற்றல்) மாற்றப்படக்கூடிய விகிதத்தைக் குறிப்பிடும் குழு விசையாகும், உதாரணத்திற்கு, ஒளியின் துடிப்பு பார்வைத்தோற்ற இழைமத்திற்கு கீழ்நோக்கி பயணமாகிறது.

நெருக்கமான சார்புடைய அளவு என்பது ஒளிவிலகல்தன்மை ஆகும், இது காற்றுமண்டல பயன்பாடுகளில் N என்று குறிப்பிடப்படுவதுடன் N = 10⁶(n - 1) என்று வரையறுக்கப்படுகிறது, காற்றின் காரணமாக 10⁶ காரணி பயன்படுத்தப்படுகிறது, n ஆனது ஆயிரத்திற்கு சில பாகங்கள் என்ற அளவில் ஒன்றுபடுதலிலிருந்து விலகுகிறது.

ஒளியின் வேகம்

வெற்றிடத்திலான எல்லா மின்காந்த கதிரியக்கத்தின் வேகமும் ஒன்றாகவே இருக்கிறது, ஏறத்தாழ 3×10⁸ மீ/வி என்பதுடன், இது c ஆல் குறிப்பிடப்படுகிறது. எனவே, v என்பது ஒரு குறிப்பிட்ட மூலப்பொருளில் உள்ள குறிப்பிட்ட நிகழ்வெண்ணின் கதரியக்கத்தினுடைய படிநிலை விசை என்றால் ஒளிவிலகல் குறிப்பானானது

n={\frac {c}{v}}

அல்லது எதிர்முகமாக

v={\frac {c}{n}}.

இந்த எண் வகைமாதிரியாக ஒன்றுக்கும் அதிகமாக இருக்கிறது: இந்த மூலப்பொருளின் அதிகபட்ச குறிப்பான் என்பது ஒளி மிக அதிகமாக வேகம் குறைவதைக் காட்டுகிறது (மேலும் பார்க்க செரன்கோவ் கதிரியக்கம்). இருப்பினும், குறிப்பிட்ட நிகழ்வெண்களில் (எ.கா. உறிஞ்சு எதிரொலிப்புகள் மற்றும் எக்ஸ் கதிர்களுக்கானவை), n உண்மையில் ஒன்றைக் காட்டிலும் சிறியதாக இருக்கும். இது தகவல்-சுமக்கும் சமிக்ஞை c யைக் காட்டிலும் எப்போதுமே வேகமாகப் பெருகக்கூடியதாக இருக்கும் என்ற சார்புநிலைக் கோட்பாட்டோடு முரண்படாது, ஏனென்றால் படிநிலை விசையானது குழு விசை அல்லது சமிக்ஞை விசைக்கு ஒன்றுபோலவே இருப்பதில்லை.

சிலபோது, ஒரு "குழு விசை ஒளிவிலகல் குறிப்பான்" வழக்கமாக குழு குறிப்பான் என்று அழைப்படுவதன் வரையறை:

n_{g}={\frac {c}{v_{g}}}

v_g என்பது குழு விசையாக இருக்குமிடத்தில். இந்த மதிப்பை எப்போதுமே படிநிலை விசையோடு வரையறுக்கப்படும் n உடன் சேர்த்து குழப்பிக்கொள்ளக்கூடாது. இந்த குழு குறிப்பானை பின்வருவனவாக ஒளிவிலகல் குறிப்பானின் அலைநீள சார்பு வகையில் எழுத முடியும்

n_{g}=n-\lambda {\frac {dn}{d\lambda }},

$\lambda$ என்பது வெற்றிடத்தின் அலைநீளமாக இருக்குமிடத்தில். நுண்ணளவுகோலில், மின்காந்த அலையின் படிநிலை விசை ஒரு பொருளில் குறைகிறது, ஏனென்றால் மின் தளமானது ஊடகத்தின் பிரிமிட்டிவிட்டிக்கு சரிவிகிதமாக உள்ள ஒவ்வொரு அணுவின் (பிரதானமாக எலக்ட்ரான்கள்) மின்னேற்றத்திலும் குறுக்கீட்டை ஏற்படுத்துகிறது. இந்த மின்னேற்றங்கள் பொதுவாக மின்னணு தளத்தை இயக்கும் விதமாக படிநிலையிலிருந்து வெளியில் சற்றே அதிகரிக்கச் செய்கின்றன. இந்த மின்னேற்றங்கள் இவ்வாறு தங்களுடைய மின்காந்த அலையை அதே நிகழ்வெண்ணில் கதிரியக்கமேற்படுத்தச் செய்கின்றன ஆனால் ஒரு படிநிலை தாமதமாக. பொருள் மீதான இதுபோன்ற பங்களிப்புகளின் மேக்ரோஸ்கோபிக் கூடுதல் அதே நிகழ்வெண்ணின் அலையாக இருக்கிறது ஆனால் அசலான அலைநீளத்தைக் காட்டிலும் குறுகலானதாக இருக்கிறது, இது அலையின் படிநிலை விசையை வேகம்குறைப்பதற்கு வழியமைக்கிறது. ஊசலாடும் பொருள் மின்னேற்றத்திலிருந்து வரும் பெரும்பாலான கதிரியக்கம் உள்வரும் அலையை மேம்படுத்தும் என்பதோடு அதனுடைய விசையையும் மாற்றுகிறது. இருப்பினும், சில மொத்த ஆற்றல் மற்ற திசைகளுக்கும் கதிரியக்கம் செய்யப்படும் (பார்க்க சிதறடித்தல்).

இரண்டு பொருட்களின் ஒளிவிலகல் குறிப்பான்கள் கொடுக்கப்பட்ட நிகழ்வெண்ணில் அறியப்பட்டதாக இருக்கிறது, இதனால் ஸநெல்ஸ் விதியின் காரணமாக முதல் பொருளிலிருந்து மற்றொன்றிற்கு மாறுகையில் ஒளிவிலகக்கூடிய நிகழ்வெண்ணின் கதிரியக்கத்தைக் கொண்டு அதன் கோணத்தைக் கணக்கிட்டுவிடலாம்.

கொடுக்கப்பட்ட பிரதேசத்தில் ஒளிவிலகல் குறிப்பான்களின் மதிப்புக்களான n அல்லது n_g ஒன்றுபடுவதிலிருந்து மாறுபடுவதாக கண்டுபிடிக்கப்படுகிறது (ஒரேவிதமானதாகவோ அல்லது தனிப்பட்டதாகவோ அல்லது ஒன்றுமில்லாததாகவோ), எனவே இந்தப் பிரதேசமானது பியாகாரே ஒத்திசைவு இல்லாதிருப்பது என்ற வகையில் வெற்றிடத்திலிருந்து தனிமைப்படுகிறது.

எதிர்மறையான ஒளிவிலகல் குறிப்பான்

$\epsilon _{r}$ மற்றும் $\mu _{r}$ ஆகிய இரண்டின் நிஜ பகுதிகள் ஒரே சமயத்தில் நேர்மறையானதாக இருந்தால் எதிர்மறை ஒளி விலகலின் குறிப்பான் தோன்றலாம் என்றும் சமீபத்திய ஆய்வுகள் நிரூபித்திருக்கின்றன, இதுபோன்றவை அத்தியாவசியமானது என்றாலும் போதுமான நிலை அல்ல. இவை இயல்பாக தோன்றுவதாக கருத முடியாது, இது செயற்கைப்பொருட்கள் எனப்படுவதைக் கொண்டு அடைய முடிவது என்பதுடன் விளைவாக கிடைக்கும் எதிர்மறை ஒளிவிலகல் (அதாவது ஓரு பின்திரும்பல் ஸ்நெல் விதி) முழுமையான ஆடிகளின் சாத்தியத்தையும் பிற அயற்பண்புள்ள நிகழ்வையும் வழங்கக்கூடியது.^[2]^[3]

சிதறடிக்கப்படுதலும் உட்கிரகிக்கப்படுதலும்

பல்வேறு கண்ணாடிகளுக்கான அலைநீளத்துடன் ஒளிவிலகல் குறிப்பானின் மாறுபாடு.

உண்மைப் பொருள்களில் எதிர் ஈர்ப்பாக்கமானது பயன்பாட்டு தளத்திற்கு உடனடியாக பதிலுரைப்பதில்லை. இது மின்கடத்தாப்பொருள் இழப்பிற்கு காரணமாகிறது, இதனை சிக்கலானதாகவும் நிகழ்வெண் சார்புடையதாகவும் உள்ள பெர்மிட்டிவிட்டி மூலம் விளக்கலாம். உண்மைப் பொருள்கள் முழுமையான மின்கடத்தாப் பொருள்கள் அல்ல, அதாவது அவை பூஜ்ஜியம்-அல்லாத நேரடி மின்சார தொடர்புத்திறனைக் கொண்டிருக்கின்றன. இரண்டு கண்ணோட்டங்களையும் பரிசீலிக்கையில் நாம் சிக்கலான ஒளிவிலகலின் குறிப்பானை வரையறுக்கலாம்:

{\tilde {n}}=n+i\kappa .

இங்கே, மேலே குறிப்பிட்டுள்ளபடி n ஆனது படிநிலை விசையை குறிப்பிடும் ஒளிவிலகல் குறிப்பானை குறிப்பிடுவதாக இருக்கிறது, அதேசமயம் κ செயலற்றுப்போன குணகம் என்றழைக்கப்படுகிறது, இது மின்காந்த அலை பொருளின் வழியாக பெருகும்போது உட்கிரகிப்பு இழப்பின் அளவைக் குறிப்பிடுகிறது. (பார்க்க ஒளி ஊடுருவலின்மையின் கணித விளக்கம்.) n மற்றும் κ ஆகிய இரண்டும் நிகழ்வெண் (அலைநீளம்) சார்ந்தவை. சிக்கலான பகுதியின் குறியீடு என்பது விதியைப் பொறுத்த விஷயம், இது இழப்பு மற்றும் லாபத்திற்கு இடையிலுள்ள சாத்தியமுள்ள குழப்பத்தின் காரணமாக முக்கியத்துவம் வாய்ந்ததாக இருக்கிறது. இயற்பியலாளர்களால் வழக்கமாக பயன்படுத்தப்படும் மேலே உள்ள குறிமாணம் கொடுக்கப்பட்டுள்ள $e^{-i\omega t}$ நேரப் பரிணாமத்தோடு தொடர்புகொண்டுள்ளதாக இருக்கிறது.

n ஆனது நிகழ்வெண்ணுடன் மாறுபடுவதன் விளைவு (எல்லா நிகழ்வெண்களும் ஒரே வேகத்தில் பயணமாகிற c வெற்றிடத்தை தவிர்த்து) சிதறடிப்பு எனப்படுகிறது, அத்துடன் இதுதான் வெள்ளை ஒளியை அது உள்ளடக்கியிருக்கும் நிறமாலை வண்ணங்களைப் பிரிப்பதற்கான கனப்பட்டைக்கு காரணமாகிறது, இதுவே வானவில்லுக்கான விளக்கமாகும் என்பதுடன் ஆடிகளில் நிறம்சார்ந்த மாறாட்டத்திற்கும் காரணமாக அமைகிறது. பொருள் உட்கிரகிக்கப்படாத நிறப்பிரிகை பிரதேசங்களில் ஒளிவிலகல் குறிப்பானின் உண்மைப் பகுதி நிகழ்வெண்ணோடு அதிகரிக்க முனைகிறது. அருகாமை உட்கிரகிப்பு உச்சமடைகிறது, ஒளிவிலகல் குறிப்பானின் வளைவு கிரேமர்ஸ்-குரோனிக் தொடர்பால் வழங்கப்பட்ட சிக்கலான வடிவத்தில் இருக்கிறது என்பதுடன் நிகழ்வெண்ணோடு குறையச்செய்கிறது.

பொருளின் ஒளிவிலகல் குறிப்பான் ஒளியின் நிகழ்வெண்ணோடு (அதன் காரணமாக அலைநீளத்தோடும்) மாறுபடுகிறது என்பதால் ஒளிவிலகல் குறிப்பான் அளவிடப்படுமிடத்தில் சம்பந்தப்பட்ட வெற்றிட அலைநீளத்தைக் குறிப்பிடுவது வழக்கமானதே. வகைமாதிரியாக, இது பல்வேறு நன்கு-வரையறுக்கப்பட்ட நிறப்பிரிகை உமிழ்வு வரிசைகளிலும் செய்யப்படுகிறது; உதாரணத்திற்கு n _D என்பது ஃபிரனாஃபர் "D" வரிசையில் ஒளிவிலகல் குறிப்பானாக இருக்கிறது, 589.29 nm அலைநீளத்தில் மஞ்சள் சோடியம் இரட்டை உமிழ்வின் மையமாக இருக்கிறது.

இந்த செல்மியர் சமன்பாடு சிதறடிப்பை விவரிப்பதில் சிறந்த அனுபவவாத சூத்திரமாக செயல்படுகிறது என்பதுடன் அட்டவணைகளில் செல்மியர் குணகங்கள் ஒளிவிலகல் குறிப்பானிற்கு பதிலாக தொடர்ந்து குறிப்பிடப்படுகின்றன. வேறுபட்ட அலைநீளங்களில் உள்ள சில பிரதிநிதித்துவ ஒளிவிலகல் குறிப்பான்களுக்கு ஒளிவிலகலின் குறிப்பான்களுடைய பட்டியலைப் பார்க்கவும்.

மேலே காட்டப்பட்டுள்ளபடி, பொருள்களிலான மின்கடத்தாப் பொருள் இழப்பு மற்றும் பூஜ்ஜியமல்லாத நேரடி மின்சார தொடர்புத்திறனானது உட்கிரகிப்பிற்கு காரணமாக அமைகிறது. கண்ணாடி போன்ற சிறந்த மி்ன்கடத்தாப் பொருள்கள் அதிகமும் குறைந்தளவு நேரடி மின்சார தொடர்புத்திறனைக் கொண்டவையாக இருக்கின்றன, அத்துடன் குறைவான நிகழ்வெண்களில் மின்கடத்தாப்பொருளின் இழப்பும் புறக்கணிக்கப்படுவதாக இருப்பது உட்கிரகிப்பு இன்மைக்கு (κ ≈ 0) காரணமாக அமைகிறது. இருப்பினும், உயர் நிகழ்வெண்களில் (புலப்படும் ஒளி போன்றவை), மின்கடத்தாப் பொருள் இழப்பு குறிப்பிடத்தகுந்த அளவிற்கு உட்கிரகிப்பை அதிகரிக்கலாம் என்பதோடு இந்த நிகழ்வெண்களுக்கான பொருளின் ஒளி ஊடுருவும் தன்மையையும் குறைக்கலாம்.

சிக்கலான ஒளிவிலகல் குறிப்பானின் கற்பனையான பாகங்கள் கிரேமர்ஸ்-குரோனிக் உறவுகளின் பயன்பாட்டின் மூலமாக தொடர்புகொண்டவையாக இருக்கின்றன. உதாரணத்திற்கு பொருளின் உட்கிரகிப்பு நிறப்பிரிகையிலிருந்து அலைநீளத்தின் செயல்பாடாக பொருளின் முழு சிக்கலான ஒளிவிலகல் குறிப்பானை ஒருவர் தீர்மானிக்கலாம்.

மின்கடத்தாப் பொருள் நிலைமாற்றமின்மைக்கான உறவு

மின்கடத்தாப் பொருளின் நிலைமாற்றமின்மை (எப்போதும் அலைநீளத்தை சார்ந்திருப்பது) ஒரு மின்காந்தமல்லாத ஊடகத்தில் ஒளிவிலகல் குறிப்பானின் சதுரமாக (சிக்கலான ஒன்றிணைப்பு சார்பு ஊடுபாவுதலோடு) இருக்கிறது. ஒளிவிலகல் குறிப்பான் ஃபிரெஸ்னல் சமன்பாடுகள் மற்றும் ஸ்நெல்ஸ் விதியில் உள்ள பார்வைத்தோற்றங்களுக்கென்று பயன்படுத்தப்படுகின்றன; அதேசமயத்தில் மின்கடத்தாப் பொருள் நிலைமாற்றமின்மை மாக்ஸ்வெல்ஸ் சமன்பாடுகளிலும் மின்னணுவியல்களிலும் பயன்படுத்தப்படுகிறது.

${\tilde {\epsilon }}$ , $\ \epsilon _{1}$ , $\ \epsilon _{2}$ , $n$ , மற்றும் $\ \kappa$ உள்ளவிடத்தில் அலைநீளத்தின் செயல்பாடுகள்:

{\tilde {\epsilon }}=\epsilon _{1}+i\epsilon _{2}=(n+i\kappa )^{2}.

பின்வருவனவற்றால் ஒளிவிலகல் குறிப்பான் மற்றும் மின்கடத்தாப் பொருள் நிலைமைற்றமின்மைக்கு இடையில் மாற்றீடு செய்யப்படுகிறது:

\ \epsilon _{1}=n^{2}-\kappa ^{2}

\ \epsilon _{2}=2n\kappa

\ n={\sqrt {\frac {{\sqrt {\epsilon _{1}^{2}+\epsilon _{2}^{2}}}+\epsilon _{1}}{2}}}

\kappa ={\sqrt {\frac {{\sqrt {\epsilon _{1}^{2}+\epsilon _{2}^{2}}}-\epsilon _{1}}{2}}}.

^[4]

வேறுபட்ட வெவ்வேறு பக்கங்கள்

ஒரு காகிதத்தின் மீது வைக்கப்பட்டுள்ள கால்சைட் கிரிஸ்டல், சில எழுத்துக்கள் இருபக்க ஒளிவிலகலைக் காட்டுகின்றன

சில குறிப்பிட்ட ஊடகத்தின் ஒளிவிலகல் குறிப்பான் எதிர் ஈர்ப்பாக்கம் மற்றும் ஊடகத்தின் வழியாக ஒளியின் பெருக்கத்தினுடைய திசையைப் பொறுத்து வேறுபடுவதாக இருக்கலாம். இது இருபக்க சிதறல் அல்லது வேறுபட்ட வெவ்வேறு பக்கங்கள் எனப்படுகிறது என்பதுடன் கிரிஸ்டல் ஆப்டிக்ஸ் துறையால் விளக்கப்படுகிறது. மிகவும் பொதுவான நிகழ்வில், மின்கடத்தாப் பொருள் நிலைமாற்றமின்மை ரேங்க்-2 டென்ஸராக இருக்கிறது (ஒரு 3க்கு 3 மேட்ரிக்ஸ்), இதனை முதன்மை அச்சுக்களோடு எதிர் ஈர்ப்பாக்கம் தவிர்த்து ஒளிவிலகல் குறிப்பான்களால் எளிதில் விளக்கிவிட முடியாது.

காந்த-கண்ணாடி (கைரோ-மேக்னடிக்) மற்றும் பார்வைத்தோற்றரீதியாக செய்லபாட்டிலிருக்கும் மூலப்பொருள்கள், முதன்மை அச்சுக்கள் ஆகியவை சிக்கலானவை (முட்டைவடி எதிர் ஈர்ப்பாக்கத்திற்கு தொடர்புடையது), அத்துடன் மின்கடத்தாப் பொருள் டென்ஸர் சிக்கலான-ஹெர்மிஷனாக இருக்கிறது (இழப்பல்லாத ஊடகம்); இதுபோன்ற பொருள்கள் நேரப்-பின்திரும்பல் ஒத்திசைவை பிரித்துவிடுகின்றன என்பதோடு ஃபாரடேயின் தனிமைப்படுத்தியை உருவாக்குவது போன்றவற்றிற்கு பயன்படுத்தப்படுகின்றன.

கிரிஸ்டலின் கால்சியம் கார்பனேட்டில் (கால்சைட்), இருபக்க சிதறல் (ஓரச்சு) பார்வைத்தோற்றங்கள் கட்டமைப்பிலுள்ள திசையாக்க வேறுபாடுகளை சார்ந்திருப்பதாக இருக்கிறது. ஒளிவிலகல்களின் குறிப்பெண்ணும் கலவையாக்கத்தை சார்ந்தே இருக்கிறது என்பதுடன் இதனை கிளேட்ஸ்டோன்-டோல் உறவைப் பயன்படுத்தி கணக்கிட முடியும்.

நேர்க்கோடின்மை

அதிக தீவிரம் வாய்ந்த ஒளியின் வலுவான மின் தளம் (லேசரின் வெளியீடு போன்றது) ஊடகத்தின் ஒளிவிலகலானது ஒளி அதன் வழியாக கடந்துசெல்லும்போது மாறுபடுவதற்கான குறிப்பானிற்கு காரணமாகலாம் என்பதோடு நேர்க்கோடற்ற பார்வைத்தோற்றங்களையும் அதிகரிக்கச் செய்கிறது. குறிப்பானானது தளத்தோடு சதுர வகையில் மாறுபடுகிறது என்றால் (தீவிரத்தன்மையோடு நேர்க்கோடாக), இது ஆப்டிகல் கெர் விளைவு எனப்படுகிறது என்பதுடன் சுய-கவனக்குவிப்பு மற்றும் சுய-படிநிலை மேம்படுத்தல் போன்ற நிகழ்வுகளுக்கு காரணமாக அமைகிறது. குறிப்பானானது தளத்தோடு நேர்க்கோட்டில் மாறுபடுகிறது என்றால் (பின்திரும்பல் ஒத்திசைவைக் கொண்டிருக்காத பொருள்களிலான ஒரே சாத்தியப்பாடு) இது பாக்கெல்ஸ் விளைவு எனப்படுகிறது.

சீரற்றதன்மை

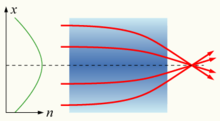
(x) ஒளிக்கதிர் தொலைவோடு உள்ள ஒளிவிலகல் குறிப்பான் (n) இன் பாராபோலிக் மாறுபாட்டுடன் கூடிய கிரேடியன்ட்-குறிப்பான் ஆடிகள். இந்த ஆடிகள் வழக்கமான ஆடிகளைப் போன்றே ஒளியை குவிமையமாக்குகின்றன.

ஒரு ஊடகத்தின் ஒளிவிலகல் குறிப்பான் நிலையானதாக இல்லாமல், ஆனால் இருக்கின்ற நிலையோடு படிப்படியாக மாறுபடுகிறது என்றால் அந்தப் பொருள் கிரேடியன்-குறிப்பான் ஊடகம் எனப்படுவதோடு இது கிரேடியண்ட் குறியீட்டெண் பார்வைத்தோற்றங்களால் விளக்கப்படுகிறது. இதுபோன்ற ஊடகத்தின் வழியாக பயணமாகும் ஒளி வளைவானதாகவோ அல்லது குவிமையம் உள்ளதாகவோ இருக்கலாம், இந்த விளைவு ஆடிகள், ஆப்டிகல் ஃபைபர் மற்றும் பிற சாதனங்களை உருவாக்க சிதறடிக்கப்படுகிறது. சில பொதுவான கானல்நீர்கள் பரவலான-அளவிற்கு மாறுபடும் காற்றின் ஒளிவிலகல் குறிப்பானால் ஏற்படுகிறது.

அடர்த்தியுடனான உறவு

ஒளிவிலகல் குறிப்பான் மற்றும் சிலிகேட் மற்றும் போரோசிலிகேட் கண்ணாடிகளின் அடர்த்திக்கும் இடையிலுள்ள உறவு.^[5]

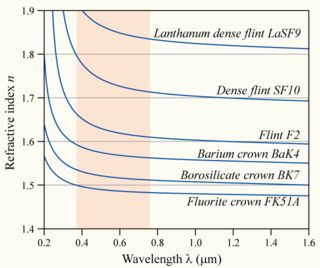
பொதுவாக ஒரு கண்ணாடியின் ஒளிவிலகல் குறிப்பான் அதனுடைய அடர்த்தியைப் பொறுத்தே அதிகரிக்கிறது. இருப்பினும், ஒளிவிலகல் குறிப்பானிற்கும் சிலிகேட் மற்றும் போரோசிலிகேட் கண்ணாடிகள் அனைத்திற்கு இடையில் ஒட்டுமொத்த நேர்க்கோட்டு உறவு என்று எதுவுமில்லை. சார்புரீதியான உயர் ஒளிவிலகல் குறிப்பான் மற்றும் குறைவான அடர்த்தி ஆகியவற்றை Li₂O மற்றும் MgO போன்ற லேசான உலோக ஆக்ஸைடுகளைக் கொண்டிருக்கும் கண்ணாடிகளைக் கொண்டு பெறலாம், அதேசமயம் எதிரான போக்கை வலதுபக்க விளக்கப்படத்தில் காணப்படுவது போன்று PbO and BaO உள்ளிட்டிருக்கும் கண்ணாடிகளைக் கொண்டு உட்கிரகிக்கப்படுகிறது.

இயங்குவிசை முரணிலை

1908 ஆம் ஆண்டில் ஹெர்மன் மின்கோவ்ஸ்கி E ஃபோட்டானின் ஆற்றலாகவும், c வெற்றிடத்தில் உள்ள ஒளியின் வேகமாகவும் n ஊடகத்தின் ஒளிவிலகல் குறிப்பானாகவும் பின்வருமாறு உள்ளவிடத்தில் ஒளிவிலகல் கதிரின் இயங்குவிசை p ஐ கணக்கிட்டார்:^[6]

p={\frac {nE}{c}}.

1909 ஆம் ஆண்டில் மாக்ஸ் ஆப்ரஹாம் இந்தக் கணக்கீட்டிற்கான பின்வரும் சூத்திரத்தை முன்வைத்தார்:^[7]

p={\frac {E}{nc}}.

ருடால்ப் பெய்ரில்ஸ் கோட்பாட்டுவாத இயற்பியலில் மிகவும் ஆச்சரியகரமானதாக உள்ள இந்த சீரற்றதன்மையை வெளிப்படுத்தினார்.^[8] செயிண்ட் ஆண்ட்ரூஸ் பல்கலைக்கழக கோட்பாட்டுவாத இயற்பியலில் தலைவராக இருக்கும் அல்ஃப் லியோன்ஹார்ட் இதைத் தீர்ப்பதற்கான பரிசோதனைகள் உட்பட இந்தப் பிரச்சினையை விவாதிக்கிறார்.^[9]

பயன்பாடுகள்

ஸ்நெல்ஸ் விதி அடிப்படையில் மைய ஆதாரத்தைச் சேர்ந்த அலைமுகப்புகள். சாம்பல்நிற கோட்டிற்கும் கீழே உள்ள பகுதி உயர் ஒளிவிலகல் குறிப்பானைக் கொண்டிருக்கிறது என்பதுடன் அதற்கு மேலே இருக்கும் குறைவான அலை விசைக்கு சரிவிகிதத்தில் இருக்கிறது.

ஒரு பொருளின் ஒளிவிலகல் குறிப்பான் ஒளிவிலகலைப் பயன்படுத்தும் எந்த ஒரு பார்வைத்தோற்ற அமைப்பின் பெரும்பாலான முக்கிய உடைமைப்பொருளாக இருக்கிறது. இது ஆடிகளின் குவிமைய சக்தியை கணக்கிடுவதற்கு பயன்படுத்தப்படுகிறது என்பதுடன் கனப்பட்டைகளின் சிதறடிப்பு சக்தியாகவும் இருக்கிறது.

ஒளிவிலகல் குறிப்பான் துணைப்பொருளின் அடிப்படை பௌதீக உடைமைப்பொருள் என்பதால் இது குறிப்பிட்ட துணைப்பொருளை அடையாளம் காணவும், அதனுடைய தூய்மையை உறுதிப்படுத்தவும், அல்லது அதனுடைய செறிவை அளவிடவும் பயன்படுத்தப்படுகிறது. ஒளிவிலகல் குறிப்பான் கெட்டிப்பொருள்கள் (கண்ணாடிகள் மற்றும் கண்ணாடிக் கற்கள்), திரவங்கள் மற்றும் வாயுக்களை அளவிடுவதற்கு பயன்படுத்தப்படுகிறது. மிகவும் பொதுவாக இது நீர்சார்ந்த கலவையில் உள்ள கலவையின் செறிவை அளவிடுவதற்கு பயன்படுத்தப்படுகிறது. ஒளிவிலகல் குறிப்பானை அளவிடுவதற்கு ஒளிவிலகல்மானி பயன்படுத்தப்படுகிறது. சர்க்கரைக்கான கலவையாக்கத்திற்கு சர்க்கரையின் உள்ளடக்கத்தை தீர்மானிக்க ஒளிவிலகல் குறிப்பான் பயன்படுத்தப்படலாம் (பார்க்க பிரிக்ஸ்).

ஜிபிஎஸ்ஸில், ஒளிவிலகலின் குறிப்பானானது பூமியின் மின் சமனாக்க காற்றுமண்டலத்தின் காரணமாக ஏற்படும் ரேடியோ பெருக்கமடைதல் தாமதத்திற்கான கதிர்-தடம்காணுதலில் பயன்படுத்தப்படுகிறது.

மேலும் பார்க்க

ஒளிவிலகல் குறிப்பான்களின் பட்டியல்
தண்ணீர் மற்றும் பனிக்கட்டியின் பார்வைத்தோற்ற உடைமைப்பொருள்கள்
செல்மியர் சமன்பாடு
மொத்த உட்புற பிரதிபலிப்பு
எதிர்மறை ஒளிவிலகல் குறிப்பான் அல்லது எதிர்மறை ஒளிவிலகல்
குறிப்பான்-பொருத்தப் பொருள்
இருபக்க ஒளிவிலகல்
கண்ணாடி உடைமைப்பொருள்களின் கணக்கீடு
எலிப்சாமெட்ரி
செயற்கைப்பொருள்
எதிர்மறை குறிப்பான் செயற்கைப் பொருள்கள்
லோரன்ட்ஸ்-லோரன்ஸ் சமன்பாடு
குறிப்பான் எலிப்சாய்ட்

குறிப்புதவிகள்

↑ Sansosti, Tanya M. (2002). "Compound Refractive Lenses for X-Rays". Stony Brook University. Archived from the original on 2018-08-11. பார்க்கப்பட்ட நாள் 2010-03-24. {{cite web}}: Unknown parameter |month= ignored (|date= suggested) (help)
↑ Hecht, Jeff (2006-12-18). "Red light debut for exotic 'metamaterial'". New Scientist Tech. Reed Business Information Ltd.
↑ "Cloaking Device Breakthrough? Negative Refraction Of Visible Light Demonstrated". ScienceDaily. ScienceDaily LLC. 2007-03-23.
↑ Wooten, Frederick (1972). Optical Properties of Solids. New York City: Academic Press. p. 49. பன்னாட்டுத் தரப்புத்தக எண் 0127634509.
↑ [9]
↑ Minkowski, Hermann (1908). "Die Grundgleichung für die elektromagnetischen Vorgänge in bewegten Körpern". Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse: 53–111. http://www.digizeitschriften.de/resolveppn/GDZPPN00250152X.
↑ Abraham, Max (1909). "Unknown". Rendiconti del Circolo matematico di Palermo 28 (1).
↑ Peierls, Rudolf (1991). More Surprises in Theoretical Physics. Princeton University Press. பன்னாட்டுத் தரப்புத்தக எண் 0691025223.
↑ Leonhardt, Ulf (2006). "Optics: Momentum in an uncertain light". Nature 444: 823–24. doi:10.1038/444823a.

வெளி இணைப்புகள்

மின்கடத்தாப் பொருள்கள்
எதிர்மறை ஒளிவிலகல் குறிப்பான் பரணிடப்பட்டது 2012-12-25 at the வந்தவழி இயந்திரம்
சயின்ஸ் வேர்ல்ட்
ஒளிவிலகல் குறிப்பான்.ஐஎன்எஃப்ஓ தரவின் ஆன்லைன் விளக்கம் மற்றும் பாராமீட்டரைசேஷனைக் கொண்டிருக்கும் ஒளிவிலகல் குறிப்பான்
sopra-sa.com பரணிடப்பட்டது 2009-02-28 at the வந்தவழி இயந்திரம் உரைக் கோப்புகளாக உள்ள ஒளிவிலகல் குறிப்பான் (தேவைக்கேற்ப அனுமதி)
தண்ணீரின் ஒளிவிலகல் குறிப்பானைத் தீர்மானிக்க உதவும் எளிய வீட்டுப் பரிசோதனை பரணிடப்பட்டது 2009-03-02 at the வந்தவழி இயந்திரம்

[1] Sansosti, Tanya M. (2002). "Compound Refractive Lenses for X-Rays". Stony Brook University. Archived from the original on 2018-08-11. பார்க்கப்பட்ட நாள் 2010-03-24. {{cite web}}: Unknown parameter |month= ignored (|date= suggested) (help)

[2] Hecht, Jeff (2006-12-18). "Red light debut for exotic 'metamaterial'". New Scientist Tech. Reed Business Information Ltd.

[3] "Cloaking Device Breakthrough? Negative Refraction Of Visible Light Demonstrated". ScienceDaily. ScienceDaily LLC. 2007-03-23.

[4] Wooten, Frederick (1972). Optical Properties of Solids. New York City: Academic Press. p. 49. பன்னாட்டுத் தரப்புத்தக எண் 0127634509.

[5] [9]

[6] Minkowski, Hermann (1908). "Die Grundgleichung für die elektromagnetischen Vorgänge in bewegten Körpern". Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse: 53–111. http://www.digizeitschriften.de/resolveppn/GDZPPN00250152X.

[7] Abraham, Max (1909). "Unknown". Rendiconti del Circolo matematico di Palermo 28 (1).

[8] Peierls, Rudolf (1991). More Surprises in Theoretical Physics. Princeton University Press. பன்னாட்டுத் தரப்புத்தக எண் 0691025223.

[9] Leonhardt, Ulf (2006). "Optics: Momentum in an uncertain light". Nature 444: 823–24. doi:10.1038/444823a.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]